ARC 123 후기

작성일 | In |

결과 및 총평

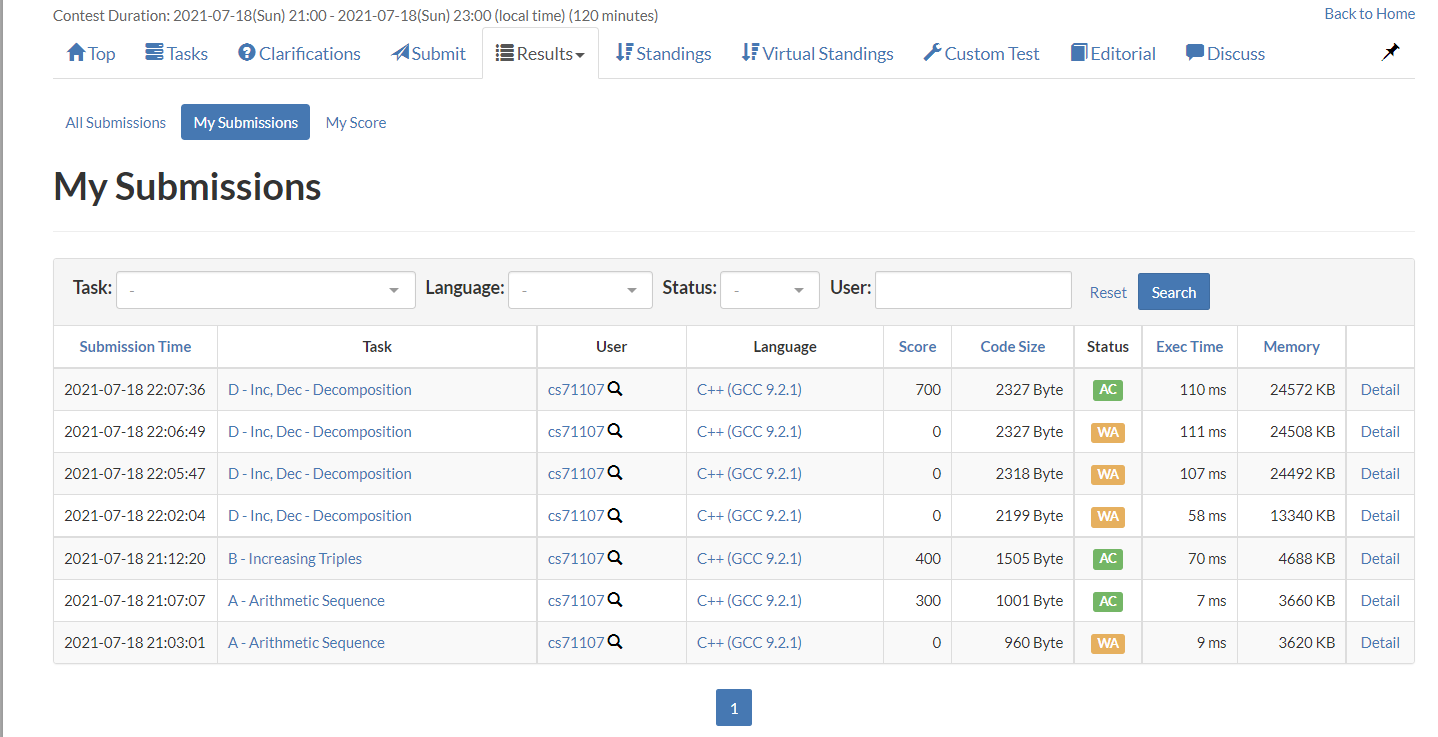
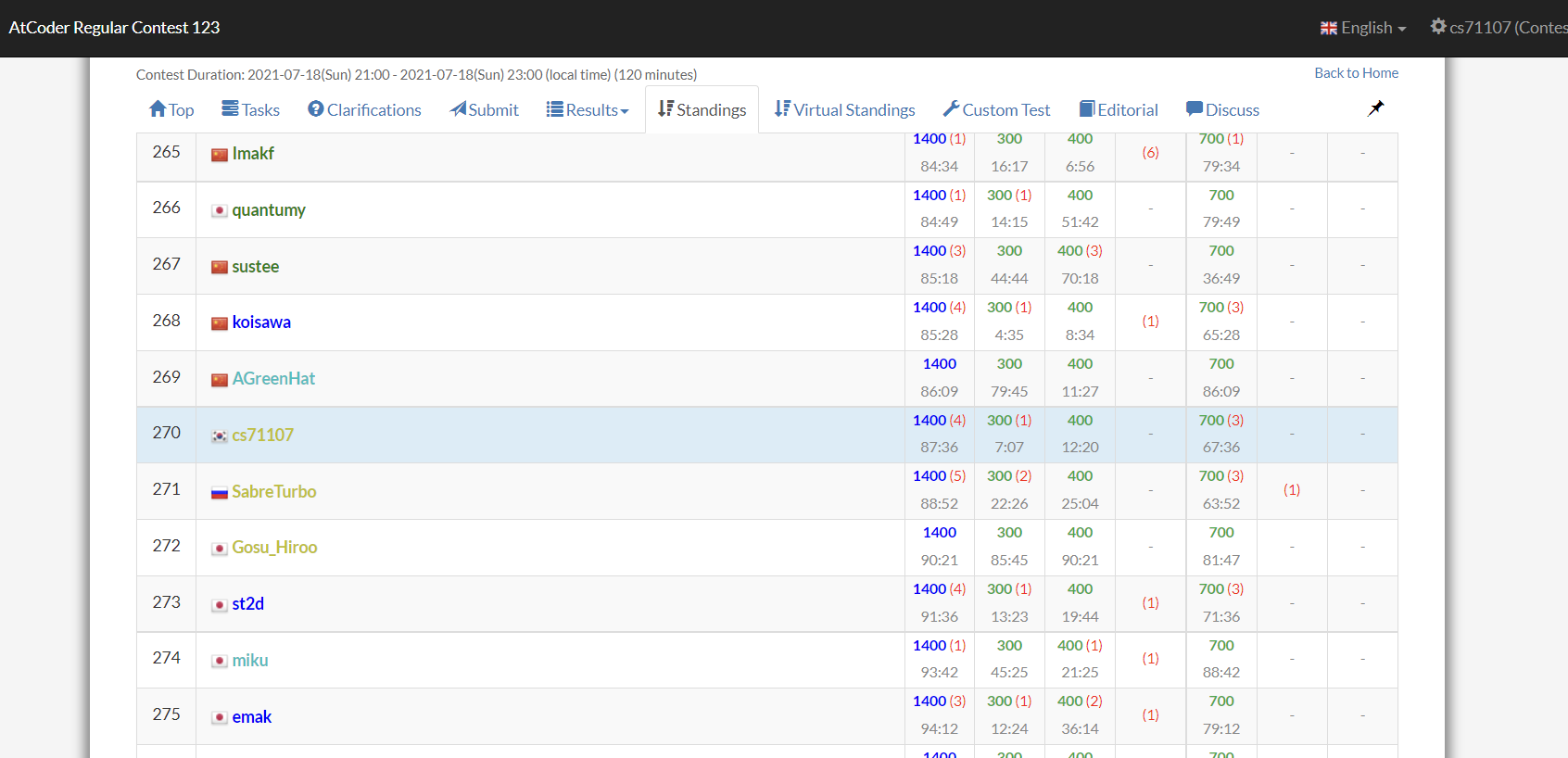
내 제출현황과 순위는 위와 같다.

썩 만족스럽지 않은 결과였다. A에서 착각을 해서 시작부터 WA를 쌓아서 시작부터 느낌이 별로 좋지는 않았다…..

순위 역시 270위로, 아주 좋지 않은 성적이다. 실제로 지난 ARC 대회와 등수만으로 비교했을 때 퍼포먼스가 현재 내 레이팅과 비슷할 것이라 여겼고, 떨어질 것이라 예상했다. 하지만 어떻게 또 올라서(….) 또 max rating을 경신했다. 다음 주에 있는 ARC는 좀 더 잘쳐서, 2200을 넘길 수 있으면 좋겠다.

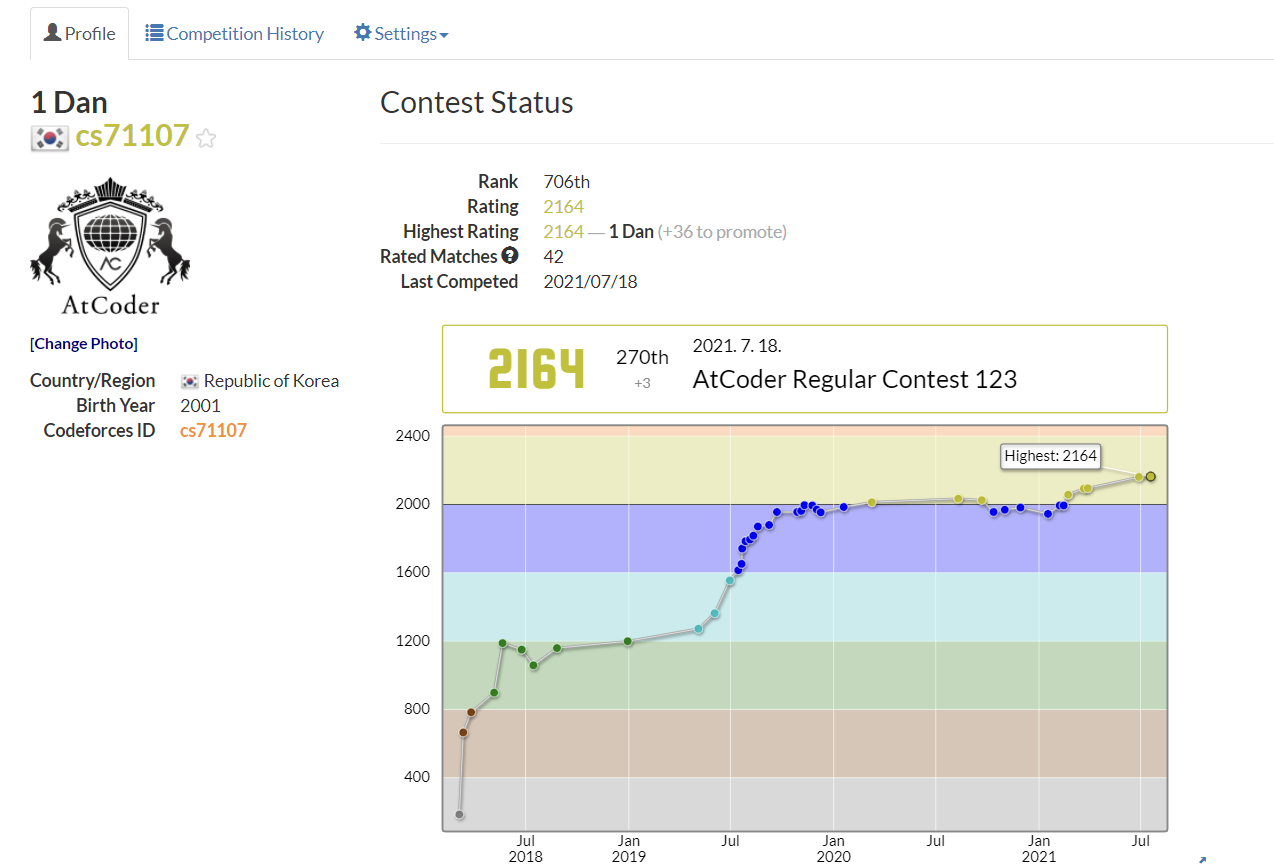
대회 문제들에 대한 얘기를 하자면 A,B는 ARC치고 좀 쉬운 난이도 였고, C,D는 살짝 어려웠다고 생각한다. C를 난 접근 조차 잘 못했고, D도 그렇게 까지 쉬운 문제는 아닌 듯. D 점수가 C 점수보다 높았고, 다행히 D를 그렇게 까지 많이 풀지 않아서 그나마 3이라도 오른 것 같다. E는 D와 점수가 같지만 어려운 문제인 듯.

아래는 A~D의 간단한 풀이와 코드이다. 이 중 C만 대회 풀이를 참고한 것이다. 문제들은 링크에서 확인 가능하다.

A. Arithmetic Sequence

세 수 $A_{0}, A_{1}, A{2}$가 주어지고, 원하는 만큼 세 수에 1씩을 더하는 연산을 시행할 수 있다. 이때, 세 수가 등차수열이 되려면 최소 몇 번을 시행해야 하는지 묻는 문제이다.

우선 편의상 $X_{0} = A_{1}-A_{0}, \ X_{1} = A_{2}-A_{1}$라고 두자. 그리고 각 $A_{i}$에 1을 더했을 때 어떤 일이 일어나는지 관찰한다.

  • $A_{0}$에 1을 더하는 경우: $X_{0}$이 1 감소한다.
  • $A_{1}$에 1을 더하는 경우: $X_{0}$이 1 증가하고, $X_{1}$이 1 감소한다.
  • $A_{2}$에 1을 더하는 경우: $X_{1}$이 1 증가한다.

위의 관찰을 응용하면, 다음과 같이 답이 나옴을 알 수 있다.

  • $X_{0} = X_{1}$인 경우, 이미 등차수열이므로 답은 $0$
  • $X_{0} > X_{1}$인 경우, $A_{0}$또는 $A_{2}$에 1을 더하면 $X_{0} - X_{1}$이 1씩 줄어들고, $A_{1}$에 1을 더하면 $X_{0} - X_{1}$이 2씩 증가한다. 그러므로, $A_{0}$또는 $A_{2}$에 1을 등차수열이 될 때까지 더하면 된다. 답은 $X_{0} - X_{1}$
  • $X_{0} < X_{1}$인 경우, $A_{0}$또는 $A_{2}$에 1을 더하면 $X_{1} - X_{0}$이 1씩 늘어나고, $A_{1}$에 1을 더하면 $X_{1} - X_{0}$이 2씩 감소한다. 그러므로 $X_{1} - X_{0}$이 짝수이면, $(X_{1} - X_{0})/2$가 답이 된다. 홀수이면, $X_{1} - X_{0}$이 1이 될 때까지 $A_{1}$에 1을 더하고, 그 후 $A_{0}, A_{1}$에 각각 1을 더하면 된다. $X_{1} - X_{0} = 2k+1$이면 답은 $k+2$이다.

이렇게 케이스를 나눠서 구현하면 끝. 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

int main()
{
    ll n,m,k,a,b,c,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    ll res = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>a>>b>>c;

    x = b-a;
    y = c-b;

    if(x==y){
        cout<<0<<"\n";
    }
    else if(x>y){
        cout<<x-y<<"\n";
    }
    else {
        k = y-x;
        if(k&1)cout<<((k>>1)+2)<<"\n";
        else cout<<(k>>1)<<"\n";
    }

    return 0;
}

B. Increasing Triples

어떤 의미에선 A보다도 쉬웠던 것 같다… 단순한 그리디가 성립한다. A를 작은 순서대로 보면서, 현재보고 있는 것보다 크면서 제일 작은 원소를 B에서 고르고, 그 고른 원소보다 크면서 제일 작은 원소를 C에서 고른 후, 이 과정을 반복한다. 더이상 그런 원소를 B또는 C에서 뽑을 수가 없으면 종료한다.

코드는 다음과 같다. 정렬 후 투 포인터처럼 순회하는 것도 가능하지만, 난 그냥 우선순위 큐를 써서 구현했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;
 
typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;
 
priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;
 
priority_queue<int> pqA;
priority_queue<int> pqB;
priority_queue<int> pqC;
 
 
int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
 
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    cin>>n;
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqA.push(-x);
    }
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqB.push(-x);
    }
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqC.push(-x);
    }
 
    int idy = -1;
 
    for(int i=0;i<n;i++){
 
        cur = -pqA.top();pqA.pop();
 
        idx = -1;
 
        while(!pqB.empty()){
            idx = -pqB.top(); pqB.pop();
            if(idx>cur)break;
        }
 
        if(idx<=cur)break;
 
        idy = -1;
 
        while(!pqC.empty()){
            idy = -pqC.top(); pqC.pop();
            if(idy>idx)break;
        }
 
        if(idy<=idx)break;
 
        cnt++;
    }
 
    cout<<cnt<<"\n";
 
    return 0;
}

C. 1, 2, 3 - Decomposition

10진법으로 나타냈을 때 $1,2,3$ 밖에 나타나지 않는 수들의 합으로 주어진 수 $N$을 나타내려면 최소 몇 개가 필요한지 묻는 문제이다.

처음 봤을 때 어떻게 접근해야 하는지 몰랐었고, 끝날 때 까지 몰랐다..

official 풀이는 다음과 같다.

$f(N)$를 원하는 값을 도출하는 함수라고 하면, $f(N) \leq K$일 조건을 생각한다. 이때, $N = 10n+r$일 때, $K \leq r \leq 3K$이고, $f(n) \leq K$ 이면 된다. 증명은 생략한다.

어쨌든 위의 사실이 성립하므로, $f(N) \leq 5$가 성립함을 알 수 있다. $K = 5$ 면 $N = 10n+r$이고, $K \leq r \leq 3K$인 $n, r$이 존재할 수 밖에 없기 때문이다.

이제 이 사실을 이용하면 메모리제이션을 이용해 문제를 풀 수 있다.

좀 더 자세한 풀이를 원한다면 editorial을 참고.

코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

map<ll,int> mp;

int solve(ll x){
    if(mp.find(x)!=mp.end())return mp[x];
    if(x<0){
        return mp[x] = INF;
    }

    int cur = (x%10);

    int res = 5;
    int curv;

    if(!cur){
        if(solve((x-10)/10)<=4)res = 4;
    }
    else if(cur==1){
        if(solve((x-10)/10)<=4)res = 4;
        curv = solve(x/10);
        if(curv<=1)res = 1;
    }
    else if(cur==2){
        if(solve((x-10)/10)<=4)res = 4;
        curv = solve(x/10);
        if(curv<=2)res = curv;
    }
    else if(cur==3){
        curv = solve(x/10);
        if(curv<=3)res = curv;
    }
    else if(cur<=6){
        curv = solve(x/10);
        if(curv<=4)res = max(curv,2);
    }
    else {
        curv = solve(x/10);
        if(curv<=4)res = max(curv,3);
    }

    return mp[x] = res;
}

int main()
{
    ll n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    mp[0] = 0;

    for(int i=1;i<=3;i++)mp[i] = 1;
    for(int i=4;i<=6;i++)mp[i] = 2;
    for(int i=7;i<=9;i++)mp[i] = 3;

    while(tc--){

        cin>>n;

        int res = solve(n);

        cout<<res<<"\n";
    }

    return 0;
}

D. Inc, Dec - Decomposition

지문이 기므로, 자세한 내용은 문제 지문을 참고.

우선, $B_{i-1} \leq B_{i}$, $C_{i-1} \geq C_{i}$라는 성질 조건 때문에, $A_{i}-A_{i-1}$ 값이 양수면 $B_{i} - B_{i-1} \geq A_{i}-A_{i-1}$이고, 음수면 $C_{i}-C_{i-1} \leq A_{i}-A_{i-1}$임이 성립함을 알 수 있다. 그리고 $B_{i}$, $C_{i}$에 대해 $(i,B_{i})$와 $(i,C_{i})$를 도시한 그래프를 생각했을 때, 구하는 값과 그래프의 개형을 생각하면 다음 성질이 성립할 때 최소가 됨을 알 수 있다.

  • $A_{i}-A{i-1} \geq 0$이면 $B_{i} - B_{i-1} = A_{i}-A_{i-1}$이 성립하고, $A_{i}-A{i-1} < 0$이면 $C_{i}-C_{i-1} = A_{i}-A_{i-1}$이다.

그리고, 이제 위의 성질이 성립한다고 생각하고, 원하는 값인 $\sum_{i=1}^{N}(\left\lvert B_{i} \right\rvert + \left\lvert C_{i} \right\rvert)를 $B_{0}$에 대한 함수로 나타내면, 직선 여러개가 붙어 있는 모양의 함수가 됨을 쉽게 알 수 있다. 따라서 변곡점에 대해서 함수 값을 모두 구한 후, 그 최솟값을 구하면 된다.

여담으로, 난 상수 최댓값 등의 범위를 잘못 정해서 세 번이나 틀렸다…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e8+10;
const int MAXN = 2e5+10;
const ll LINF = 1LL*INF*MAXN;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

ll A[MAXN];
ll B[MAXN];
ll C[MAXN];
int cal[MAXN*3];
ll vv[MAXN*3];
char S[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++){
        cin>>A[i];
    }

    for(int i=1;i<n;i++){
        if(A[i]>A[i-1]){
            B[i] = A[i]-A[i-1];
        }
        else {
            C[i] = A[i]-A[i-1];
        }
    }

    for(int i=1;i<n;i++){
        B[i]+=B[i-1];
        C[i]+=C[i-1];
    }

    vector<ll> pos;

    pos.push_back(-LINF);
    pos.push_back(LINF);

    for(int i=0;i<n;i++){
        pos.push_back(-B[i]);
        pos.push_back(-B[i]-1);
        pos.push_back(-B[i]+1);
        pos.push_back(A[0]+C[i]);
        pos.push_back(A[0]+C[i]-1);
        pos.push_back(A[0]+C[i]+1);
    }

    sort(pos.begin(),pos.end());
    pos.erase(unique(pos.begin(),pos.end()),pos.end());

    ll totv = 0;

    for(int i=0;i<n;i++){
        idx = lower_bound(pos.begin(),pos.end(),-B[i])-pos.begin();
        cal[idx]++;
        vv[idx]+=B[i];
        idx = lower_bound(pos.begin(),pos.end(),A[0]+C[i])-pos.begin();
        cal[idx]++;
        vv[idx]-=(A[0]+C[i]);

        totv -= B[i];
        totv += (A[0]+C[i]);
    }

    int psz = (int)pos.size();

    ll va = -(n<<1);

    ll res = 300LL*INF*INF;
    ll curv = 0;

    for(int i=0;i<psz-1;i++){

        va += (cal[i]<<1);
        totv += (vv[i]<<1);

        curv = va*pos[i]+totv;

        res = min(res,curv);
    }

    cout<<res<<"\n";

    return 0;
}