UCPC 2021 본선 후기 및 풀이

작성일 | In |

들어가기 전에

UCPC 본선은 올해 8월 14일에 있었고, 이 글을 쓰는 지금이 11월 17일이니까, 무려 3달이 넘었다. 그동안 본선 후기를 못 쓴 핑계를 대자면, 대회가 끝나고 얼마 지나지 않아서 랩 인턴 지원이라던가, 정보처리산업기사 시험 접수라던가 하는 일들이 있었고, 학기 때는 학기와 ICPC에 이리 치이고 저리 치여서 후기를 쓰지 못했다.

이제 ICPC도 끝났고, 학기 관련해서도 중간고사가 끝나고 과제도 당장 급한 게 없어서, 늦었지만 후기를 써보려 한다.

최대한 정확하게 쓰려 하지만, 시간이 오래 지났기 때문에 부정확할 수 있다. 양해 바란다.

대회 준비 과정

앞선 UCPC 예선의 결과가 굉장히 좋은 편이었기 때문에 (4위), 본선에도 높은 순위를 기대할 수 있지 않을까? 하는 기대가 있었다.

예선과 본선 간에 약 2주의 시간이 있었고, 방학이었으나, 각자 일정 때문에 연습을 그리 많이 잡지는 못했다.

UCPC는 3컴이었기 때문에 모이지 않고, 디스코드와 각자 컴을 사용해서 연습 했다.

본선 연습으로는 2017 Tsukuba regional과, GCPC 2019를 돌았다.

이때 팀연습 결과를 첨부한다.

2017 Tsukuba:

GCPC 2019:

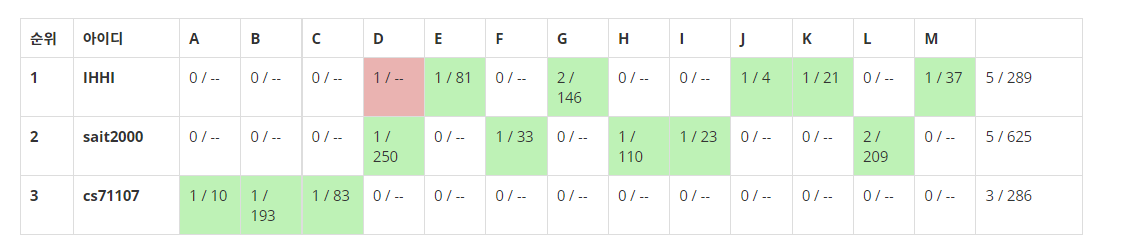
위의 결과에서 볼 수 있다시피 2017 Tsukuba의 경우 solved.ac 기준 다이아 2 이상 문제를 제외한 모든 문제를 풀었고, GCPC 2019의 경우 올솔브를 했다.

그래서 UCPC 본선도 기대하며 준비할 수 있었다. 다만, 위의 결과에서 보다시피 내 기여가 좀 적었기 때문에… 난 본선에선 좀 더 기여를 하자고 다짐하면서 준비했다.

대회 진행 과정

대회 장소는 서울대의 윗공대 301동의 slab이란 곳으로 정했다. 시간은 대회 당시 시간 (KST 기준)이다.

11:00 - 대회시작, 평소대로 내가 A,B,C,D를 Sait신이 E,F,G,H를 , 그리고 IHHI가 I,J,K,L을 잡았다.

11:00 ~ 11:20 - 대회시작 부터 이때까지, 문제들이 전체적으로 쉽지 않다는 것을 깨달았다. A의 경우 대략적인 풀이를 알아냈지만, 그것을 구체화 시키고 구현하는 것보단 그냥 넘어가는게 맞다는 판단을 내렸다 그리고 B,C를 읽었지만 풀이에 접근조차 하지 못했다. 대충 분위기를 확인해보니까 다른 팀원들도 비슷한 분위기 같았다. (나중에 solve.ac 기준 난이도를 보니 Sait님의 H가 유일한 골드였고, IHHI는 잡았던 문제 중 가장 쉬운 문제가 플1 이었다.)

11:20 - D를 읽고 나서 빠르게 구현하면 되는 문제라는 것을 알아냈고, 구현했다. 바로 AC. 이때부터 난 A를 구현하기 시작했다.

11:29 - Sait님이 H가 적당히 풀만한 문제이나, 본인은 빠르게 구현할 자신이 없다고 하시며 IHHI에게 토스. IHHI가 구현해서 AC.

12:03 - D 이후 A를 내가 꾸준히 구현하고 있었고, 구현을 끝낸 후 제출 한번만에 AC를 받았다.

12:29 - 내가 A관련해서 씨름할 때 Sait신이 K를 읽은 후 이거 킹전 지식 문젠데?를 시전하셨고, 나도 처음들어보는 사전 지식을 언급하며 이걸 알면 케이스 워크라고 하시면서 슥슥 구현하고 계셨고, IHHI는 J를 잡고 구현하고 있었다. 그리고 IHHI는 J를 제출했찌만 아쉽게 WA가 떴고, 거의 바로 Sait신이 K를 퍼솔했다.

12:36 - IHHI가 J를 고쳐서 맞았다. 5솔.

12:36 ~ 13:18 - 이제 대충 풀만한 문제가 어떤 문제들인지 대충 나온 상태였기 때문에, Sait,IHHI가 E를 고민하고, 난 F를 잡았다. F를 보니 Taxi 거리의 성질을 이용하면 되는 문제라고 판단했다. 단, 내 풀이는 구현이 좀 걸렸다. 하지만 그때 당시 이 풀이를 빠르게 이해하고 구현할 수 있는 사람이 나라서, 그냥 내가 구현하기로 했다.

13:18 - 짜고 난 코드를 돌려보니 예제컷이 나서 멘붕을 경험한 후 코드를 좀 고치니 바로 예제가 나왔고, 그냥 제출했다. AC.

13:18~13:54 - 스코어 보드 상에선 E가 많이 풀려있었기 때문에, E를 빠르게 밀어야 한다는 판단을 했다. 나와 IHHI, Sait이 모두 고민했다. 그러던 중 IHHI가 그냥 이렇게 가면 되는 것 아니냐?라고 한 후 구현을 시작했다.

13:54 - E 구현을 마친 후 AC.

13:54 ~ 종료 시까지 - 대충 스코어보드를 봤을 때, B,L은 사람이 풀게 아니다!라는 결론을 내렸고, Sait님은 자기분야?인 G를 계속 고민했으나 이거다 하는 풀이를 찾지 못하고 있었다. 결국 도전할 만한 건 C,I 였고, 구현 문제 같은 C를 IHHI, Sait이 맡고, I를 내가 가져가기로 하고 각자 고민과 구현을 시작했다. 그러나 종료 5분전 제출한 내 구현은 여지 없이 WA가 나왔고, IHHI,Sait이 각자 C를 구현했으나 제한 시간 내에 구현하지 못했다. 그리고 그대로 대회가 끝났다.

대회 결과

비록 C,I를 못 풀긴 했으나, 높은 순위일 것으로 예측하고 있었고, 우린 정리를 한 후 윗공대 명물(?)인 300동 식당에서 저녁을 먹었다. 저녁을 먹으면서 못 푼 문제들 풀이를 들으니 C는 구현이 맞았고, I는 놀랍게도(?) 플로우여서 좀 허탈했다.

그리고 스코어보드 까는 방송을 시청했다.

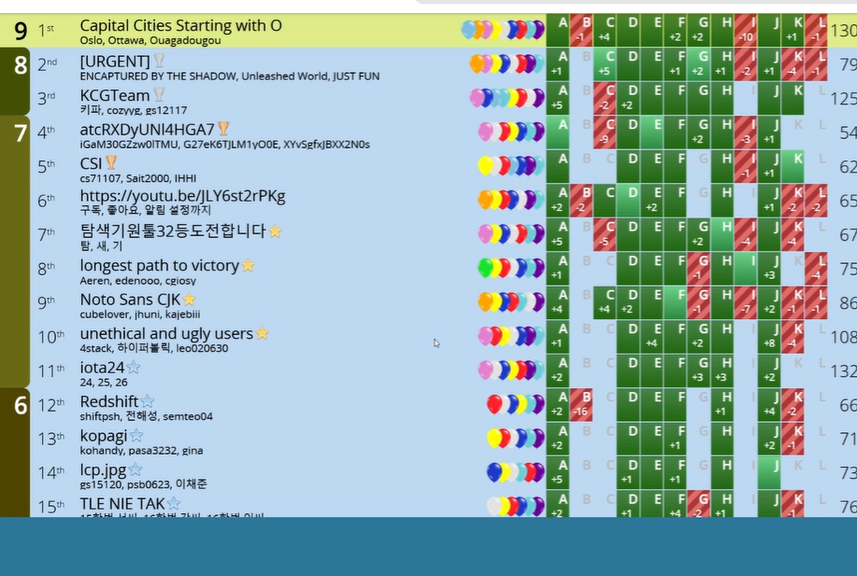
그리고 결과는 다음과 같이 5위(!!!)라는 매우 높은 수상을 받을 수 있었다.

7솔브 팀이 꽤 많았는데, 우리 팀 패널티 관리가 나쁘지 않았던 것 같다.

대회 총평

UCPC 2021 도 solved.ac 기준 골드 1 - 플레 5 - 다이아 3 - 루비 1이라는 어려운 셋이었다.

하지만 초반에 말리지 않고 각자 역할 분배를 확실하게 해서 패널티를 줄이고, 무엇보다 Sait신이 K를 퍼솔해준 게 수상에 큰 역할을 했다.

그리고 이번 셋에선 내가 혼자서 3개를 밀었기 때문에 유의미한 기여를 했고, IHHI 역시 3개를 풀었다. 그리고 Sait신은 비록 K하나를 풀었지만, 수상 결정에 있어서 가장 중요했던 K를 풀어주는 역할을 수행했다.

각자가 잘하는 것들을 잘 분배해서 해결한 것이 높은 순위를 가져온 동력이 됐다고 생각한다.

5등상 상품은 데브시스터즈에서 지원해줬다. 에어팟 잘 쓰겠습니다~

문제 풀이

출제된 문제들 중 내가 백준에서 푼 것들에 대해서 풀이를 작성한다.

다른 문제들의 경우 내가 업솔빙을 진행함에 따라 여기에 업데이트 할 것 같다.

문제들은 여기에서 확인가능하다.

A. A+B와 쿼리

문제를 요약하면, A,B 두 10진수 정수가 있고(크기가 아주 크다.) A,B의 특정 자리수를 바꾸는 쿼리가 주어진다.

그리고 쿼리가 주어질 때마다, C = A+B를 계산한 후, 쿼리가 주어지기 이전과 비교해서 ‘달라진 자릿수의 개수’가 몇개인지 묻는 문제이다.

우선 우리가 신경 써야 할 것이 받아올림이란 것은 쉽게 생각할 수 있다.

편의상 A,B를 각 원소가 0~9인 길이 N 짜리 정수 배열로 보자. 그리고 $i$ 번째 자리수를 $A[i],B[i]$라고 두자.

그리고 문제의 조건상, 각 자릿수에 대해서 생각하면 그 전에 올라오는 자릿수의 받아 올림 값은 0,1 중에 하나다.

그럼 각 자릿수에 해당하는 수들의 합에 따라 케이스를 나눠 보자.

$A[i]+B[i] \geq 10$인 경우 : 올라오는 자릿수의 받아 올림 값에 상관 없이 1을 올린다.

$A[i]+B[i] = 9$인 경우 : 올라오는 자릿수의 받아 올림 값에 따라 넘기는 값이 바뀐다.

$A[i]+B[i] \leq 8$인 경우 : 올라오는 자릿수의 받아 올림 값에 상관 없이 0을 올린다.

이렇게 경우를 나눠서 생각하면 받아 올림이 계속 올라가다가 첫번째, 세번째 케이스에 해당하는 경우를 처음 만났을 때, 이전 결과에 대해 자릿수가 바뀌는 경우가 끝난다는 것을 알 수 있다.

즉 우리가 해줘야 하는 것은

  • 각 $i$에 대해 $A[i]+B[i]$가 위의 3가지 경우 중 어디에 속하는지 관리
  • 그 관리하는 정보를 바탕으로 문제에서 원하는 정답을 구하기

로 나눌 수 있다.

현재 쿼리에 의해 업데이트가 일어나고, 전체 배열에 대해 답을 빠르게 구해야 하므로, 세그 트리(또는 인덱스 트리)를 통해서 관리해줘야 겠다는 생각을 할 수가 있고 실제로 가능하다.

업데이트가 들어올 때마다 결과가 어떻게 바뀌는지 계산하고, 현재 자리수에 해당하는 경우가 1,3번째인지, 2번째인지에 따라 업데이트한다.

계산의 경우 현재 업데이트에 의해서 1,3번째경우에서 2번째 경우로 바뀌는지 또는 그 반대인지 여부를 검사하고, 그에 따라 답을 계산한다.

자세한 계산은 코드를 참고하라. 구간의 min을 계산하는 IDT와 max를 계산하는 IDT를 사용하고 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 3e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int B[MAXN];
char S[MAXN];
char T[MAXN];

int tree[MAXN*4];
int ttree[MAXN*4];

inline void update(int tmp,int v,int vv){

    tree[tmp] = v;
    ttree[tmp] = vv;

    tmp>>=1;

    while(tmp){
        tree[tmp] = max(tree[(tmp<<1)],tree[(tmp<<1)|1]);
        ttree[tmp] = min(ttree[(tmp<<1)],ttree[(tmp<<1)|1]);
        tmp>>=1;
    }

    return;
}

inline int getmx(int L,int R){

    int res = -INF;

    while(L<=R){
        if(L&1){
            res = max(res,tree[L]);
            L++;
        }
        if(!(R&1)){
            res = max(res,tree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}


inline int getmn(int L,int R){

    int res = INF;

    while(L<=R){

        if(L&1){
            res = min(res,ttree[L]);
            L++;
        }
        if(!(R&1)){
            res = min(res,ttree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}

inline int isup(int idx,int base){

    if(A[idx]+B[idx]<9)return 0;

    if(A[idx]+B[idx]>9)return 1;


    int ii = getmn(base+idx+1,(base<<1)-1);

    if(ii==INF)return 0;
    else if(A[ii]+B[ii]<9)return 0;
    else return 1;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    char ty;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>q;

    cin>>S+1;
    cin>>T+1;

    int base = 1;

    for(;base<=n;base<<=1);

    tree[base] = 0;
    ttree[base] = 0;

    for(int i=1;i<=n;i++){
        A[i] = S[i]-'0';
        B[i] = T[i]-'0';

        if(A[i]+B[i]==9){
            tree[base+i] = -INF;
            ttree[base+i] = INF;
        }
        else {
            tree[base+i] = i;
            ttree[base+i] = i;
        }
    }

    for(int i=n+1;i<base;i++){
        tree[base+i] = -INF;
        ttree[base+i] = INF;
    }

    for(int i=base-1;i>=1;i--){
        tree[i] = max(tree[(i<<1)],tree[(i<<1)|1]);
        ttree[i] = min(ttree[(i<<1)],ttree[(i<<1)|1]);
    }

    int v;

    int preup = 0;
    int curup = 0;

    int res = 0;
    int curidx = -1;

    for(int i=0;i<q;i++){
        cin>>ty>>idx>>v;

        idx = (n-idx+1);

        if(ty=='A'){
            if(A[idx]==v){
                cout<<0<<"\n";
            }
            else {

                preup = isup(idx,base);

                A[idx] = v;

                curup = isup(idx,base);

                if(preup^curup){
                    curidx = getmx(base,base+idx-1);
                }
                else {
                    curidx = idx;
                }

                cout<<(idx-curidx+1)<<"\n";

                if((A[idx]+B[idx])==9)update(base+idx,-INF,INF);
                else update(base+idx,idx,idx);
            }
        }
        else {
            if(B[idx]==v){
                cout<<0<<"\n";
            }
            else {

                preup = isup(idx,base);

                B[idx] = v;

                curup = isup(idx,base);

                if(preup^curup){
                    curidx = getmx(base,base+idx-1);
                }
                else {
                    curidx = idx;
                }

                cout<<(idx-curidx+1)<<"\n";

                if((A[idx]+B[idx])==9)update(base+idx,-INF,INF);
                else update(base+idx,idx,idx);
            }
        }
    }


    return 0;
}

D. 츠바메가에시

문제 설명은 생략한다.

결국 경우의 수가

  • x 축에 평행한 3개
  • x 축에 평행한 것 2개에 y 축에 평행한 것 1개
  • x 축에 평행한 것 1개에 x 축에 평행한 것 2개
  • y 축에 평행한 것 3개

이 4가지 경우 밖에 없음을 알 수 있다.

이 4가지 각각에 대해서 전부 해당 경우의 답을 계산하면 되는데,

앞의 두 개를 계산 가능하면 뒤에 두 개도 비슷하게 계산 가능하므로 앞의 두 개만 설명한다.

x 축에 평행한 3개의 경우 각 y 좌표에 대해 값들의 합을 저장하는 배열을 만들고 입력을 순회하면서 계산 해준뒤, 중복이 생기지 않게 주의하면서 가장 합이 큰 3개의 합을 구하면 된다.

x 축에 평행한 것 2개에 y 축에 평행한 것 1개의 경우 우선 y 축에 평행한 것 1개를 기준으로 생각한다.

각 x 좌표를 순회하면서, y축에 평행한 참격의 좌표를 현재 좌표로 했을 때, x 축에 평행한 참격 2개를 한다고 할 때의 얻는 최댓값을 계산하면 된다. 겹치는 제비의 경우, 한번만 세지므로, 해당 x 좌표의 제비들을 계산하기 전에 미리 제거 한 후, 그때의 답을 계산하고, 다음 좌표로 넘어갈 때 다시 복원시켜준다고 생각하면 풀이의 방향을 잡기 쉽다.

따라서 이 문제도 업데이트와 계산이 필요한 문제로 바꿀 수 있고, 이는 세그 트리 및 오프라인 쿼리를 사용해서 계산 가능하다.

코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e6+10;
const int MAXM = 1e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int yv[MAXN];
int xv[MAXN];

vector<pii> xval[MAXN];
vector<pii> yval[MAXN];

pii tree[MAXN*4];

inline void update(int tmp,int v){

    tree[tmp].f+=v;
    tmp>>=1;

    while(tmp){

        if(tree[(tmp<<1)].f>tree[(tmp<<1)|1].f){
            tree[tmp].f = tree[(tmp<<1)].f;
            tree[tmp].s = max(tree[(tmp<<1)].s,tree[(tmp<<1)|1].f);
        }
        else {
            tree[tmp].f = tree[(tmp<<1)|1].f;
            tree[tmp].s = max(tree[(tmp<<1)|1].s,tree[(tmp<<1)].f);
        }

        tmp>>=1;
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    int xmx = 0;
    int ymx = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++)
    {
        cin>>x>>y>>a;
        xval[x].push_back(pii(y,a));
        yval[y].push_back(pii(x,a));
        xv[x]+=a;
        yv[y]+=a;
        xmx = max(xmx,x);
        ymx = max(ymx,y);
    }

    int res = 0;

    int mx1 = 0,mx2 = 0;

    for(int i=0;i<=xmx;i++){
        cur = xv[i];
        if(mx<cur){
            mx2 = mx1;
            mx1 = mx;
            mx = cur;
        }
        else if(mx1<cur){
            mx2 = mx1;
            mx1 = cur;
        }
        else {
            mx2 = max(mx2,cur);
        }
    }

    res = max(res,(mx+mx1+mx2));

    mx = 0;
    mx1 = 0;
    mx2 = 0;

    for(int i=0;i<=ymx;i++){
        cur = yv[i];
        if(mx<cur){
            mx2 = mx1;
            mx1 = mx;
            mx = cur;
        }
        else if(mx1<cur){
            mx2 = mx1;
            mx1 = cur;
        }
        else {
            mx2 = max(mx2,cur);
        }
    }

    res = max(res,(mx+mx1+mx2));

    int base = 1;

    for(;base<=ymx;base<<=1);

    for(int i=0;i<=ymx;i++){
        tree[i+base] = pii(yv[i],0);
    }

    for(int i=ymx+1;i<base;i++){
        tree[i+base] = pii(0,0);
    }

    for(int i=base-1;i>=1;i--){
        if(tree[(i<<1)].f>tree[(i<<1)|1].f){
            tree[i].f = tree[(i<<1)].f;
            tree[i].s = max(tree[(i<<1)].s,tree[(i<<1)|1].f);
        }
        else {
            tree[i].f = tree[(i<<1)|1].f;
            tree[i].s = max(tree[(i<<1)|1].s,tree[(i<<1)].f);
        }
    }

    for(int i=0;i<=xmx;i++){
        for(int j=0;j<(int)xval[i].size();j++){
            idx = xval[i][j].f;
            cur = xval[i][j].s;

            update(base+idx,-cur);
        }

        res = max(res,xv[i]+tree[1].f+tree[1].s);

        for(int j=0;j<(int)xval[i].size();j++){
            idx = xval[i][j].f;
            cur = xval[i][j].s;

            update(base+idx,cur);
        }
    }

    base = 1;

    for(;base<=xmx;base<<=1);

    for(int i=0;i<=xmx;i++){
        tree[i+base] = pii(xv[i],0);
    }

    for(int i=xmx+1;i<base;i++){
        tree[i+base] = pii(0,0);
    }

    for(int i=base-1;i>=1;i--){
        if(tree[(i<<1)].f>tree[(i<<1)|1].f){
            tree[i].f = tree[(i<<1)].f;
            tree[i].s = max(tree[(i<<1)].s,tree[(i<<1)|1].f);
        }
        else {
            tree[i].f = tree[(i<<1)|1].f;
            tree[i].s = max(tree[(i<<1)|1].s,tree[(i<<1)].f);
        }
    }

    for(int i=0;i<=ymx;i++){
        for(int j=0;j<(int)yval[i].size();j++){
            idx = yval[i][j].f;
            cur = yval[i][j].s;

            update(base+idx,-cur);
        }

        res = max(res,yv[i]+tree[1].f+tree[1].s);

        for(int j=0;j<(int)yval[i].size();j++){
            idx = yval[i][j].f;
            cur = yval[i][j].s;

            update(base+idx,cur);
        }
    }

    cout<<res<<"\n";

    return 0;
}

E. 가위바위보 정렬

문제 설명은 역시 생략한다.

우선 $O(NT)$ 의 알고리즘으로는 당연히 시간내에 돌아가게 할 수 없다.

하지만 특수한 경우를 생각해보면, 3가지 모두 있는 케이스가 아니라 특정 2가지 종류만 있는 케이스에 대해선 답을 알아낼 수 있다.

이 경우는 같은 카드끼리 묶은 후, 횟수와 묶음의 개수에 따라서 적절히 답을 계산 가능하다. (코드 참고)

이제 3가지 경우가 다 있는 케이스가 문제인데, 이 경우는 위 처럼 2가지 경우만 있는 배열 몇개로 분할이 가능하다는 것을 보임으로써 해결 가능하다.

앞에서부터 배열($A$)을 본다고 할 때, 3가지 경우 (가위,바위,보)가 전부 나오는 최초의 시점을 생각하자. (그 지점을 $i$라고 한다.)

그럼 $A[1…(i-1)]$과 $A[i…]$가 섞이지 않는다는 것을 증명할 수 있다. 자세한 증명은 연습으로 남긴다.

그럼 이제 2가지 경우만 있는 배열 몇 개로 전체 배열을 분할 할 수 있고 (마지막 배열의 경우 1가지만 있을 수 있다.)

각각에 대해서 답을 계산해주면 원하는 답을 얻을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 5e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

pii A[MAXN];

char val[10] = {'S','R','P'};

char S[MAXN];
char T[MAXN];

int curidx = 0;

void solve(int a,int b,int k){

    if(a==b){

        for(int j=1;j<=A[a].s;j++){
            T[curidx+j] = val[A[a].f];
        }
        curidx+=A[a].s;

        return;
    }

    int va = A[a].f;
    int vb = A[a+1].f;
    
    int wv = 0;

    if(((va+1)%3) == vb){
        wv = vb;
    }
    else {
        wv = va;
    }

    int cnt = 0;

    int cur = 0;
    int ccal = 0;

    for(int i=a;i<=b;i++){

        cur = A[i].f;
        ccal = A[i].s;

        if(cur^wv){
            for(int j=1;j<=ccal;j++){
                T[curidx+j] = val[cur];
            }
            curidx+=ccal;
        }
        else {

            if(cnt>=k){
                for(int j=1;j<=ccal;j++){
                    T[curidx+j] = val[cur];
                }
                curidx+=ccal;
            }
            else if(cnt+ccal>=k){
                for(int j=1;j<=(cnt+ccal)-k;j++){
                    T[curidx+j] = val[cur];
                }
                curidx += (cnt+ccal)-k;

                cnt = k;
            }
            else {
                cnt += ccal;
            }
        }
    }

    for(int j=1;j<=cnt;j++){
        T[curidx+j] = val[wv];
    }
    curidx+=cnt;

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>k;

    cin>>S+1;

    cnt = 1;
    idx = 0;

    for(int i=2;i<=n;i++){
        if(S[i]==S[i-1]){
            cnt++;
        }
        else {
            idx++;
            if(S[i-1]=='S'){
                A[idx] = pii(0,cnt);
            }
            else if(S[i-1]=='R'){
                A[idx] = pii(1,cnt);
            }
            else {
                A[idx] = pii(2,cnt);
            }

            cnt = 1;
        }
    }

    idx++;
    if(S[n]=='S'){
        A[idx] = pii(0,cnt);
    }
    else if(S[n]=='R'){
        A[idx] = pii(1,cnt);
    }
    else {
        A[idx] = pii(2,cnt);
    }


    int bi = 0;
    int pre = 1;

    for(int i=1;i<=idx;i++){
        cur = A[i].f;
        if((bi|(1<<cur))==7){
            solve(pre,i-1,k);
            pre = i;
            bi = (1<<cur);
        }
        else {
            bi|=(1<<cur);
        }
    }

    solve(pre,idx,k);

    cout<<T+1<<"\n";

    return 0;
}

F. 간단한 문제

제목 처럼 (알고 보면) 간단한 문제 이다.

우선 두 정수 $x,y$에 대해 다음 성질이 성립한다는 것은 자명하다.

$x+y = min(x,y)+max(x,y)$ 그러므로, 문제에서 구해야 하는 식을 다음과 같이 변경 시키는 것이 가능하다.

$min({\left\lvert {p_{i}-p_{j}} \right\rvert},{\left\lvert {q_{i}-q_{j}} \right\rvert}) = ({\left\lvert {p_{i}-p_{j}} \right\rvert}+{\left\lvert {q_{i}-q_{j}} \right\rvert})-max({\left\lvert {p_{i}-p_{j}} \right\rvert},{\left\lvert {q_{i}-q_{j}} \right\rvert})$

$min$에서 $max$로 바뀐 것이 무슨 의미가 있냐고 생각할 수 있지만, 중요한 의미가 있다.

일반적으로 두 점 $(a,b)$와 $(x,y)$에 대해서 $dist = {\left\lvert {a-x} \right\rvert}+{\left\lvert {b-y} \right\rvert}$로 거리를 정의하면, $a_{1} = (a+b), b_{1} = (a-b), x_{1} = (x+y), y_{1} = (x-y)$라고 했을 때, $dist = max({\left\lvert {a_{1}-x_{1}} \right\rvert},{\left\lvert {b_{1}-y_{1}} \right\rvert})$라는 성질이 성립한다. (이에 대한 더 자세한 내용을 알고 싶으면 택시 기하를 검색해보기 바란다.)

그렇다면 이제 위의 성질을 알고 있으니, 주어진 식의 변형에서 max에 관련된 식을 다시 절댓값의 합으로 풀어줄 수 있다.

풀어주면 그걸 계산하는 건 간단한 정렬을 통해서 계산 가능하다. 하지만 대회 중엔 위의 성질을 통해 식만 변형하고, 세그 트리를 통해 복잡하게 풀었다….

아래의 코드는 나중에 작성한 간단한 풀이의 코드. 복잡한 코드는 이 문제를 맞으면 내 제출현황에서 볼 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e6+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int B[MAXN];

ll val[MAXN];

ll getans(int n)
{
    sort(val+1,val+n+1);

    ll res = 0;
    ll tot = 0;
    ll curv = 0;

    for(int i=1;i<=n;i++){
        tot += val[i];
    }

    for(int i=1;i<=n;i++){
        curv += val[i];

        res += (i*val[i]-curv);
        res += ((tot-curv)-(n-i)*val[i]);
    }

    return res;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>A[i];
    }

    for(int i=1;i<=n;i++){
        cin>>B[i];
    }

    ll res = 0;
    ll totv = 0;
    ll vv = 0;

    for(int i=1;i<=n;i++){
        val[i] = A[i];
    }

    totv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = B[i];
    }

    totv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = (A[i]+B[i]);
    }

    vv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = (A[i]-B[i]);
    }

    vv += getans(n);

    vv>>=1;

    res = totv-vv;

    cout<<res<<"\n";

    return 0;
}

H. 봉화대

문제 설명은 생략.

dp를 생각해보자. $dp[i]$를 $i$번째 봉우리까지 생각할 때 구간을 나누는 개수라고 생각하자.

현재 봉우리의 높이가 $1$이상 $N$ 이하의 서로 다른 정수이므로, $id[i]$를 높이가 $i$인 봉우리의 위치로 정의하고, $mxv[i]$를 $1$번째 봉우리 부터 $i$번째 봉우리까지의 높이 중 최댓값으로 정의하자.

$dp[i]$를 계산하기 위해 $i$번째 봉우리가 속하는 구간을 살펴보면 $id[mxv[i]]$번째 봉우리와 무조건 같은 구간에 속해야 한다는 것을 알 수 있다. 그리고, 저 봉우리와 같은 구간에 속하기만 한다면, 적어도 $i$번째 봉우리가 속하는 구간은 문제가 없다. 그러므로, $psum[i]$를 $dp[i]$의 누적합으로 정의한다면, $dp[i] = psum[id[mxv[i]]-1]$라는 등식이 성립함을 알 수 있다.

전처리에 $O(n)$, $dp$값 계산에 $O(n)$만에 계산이 가능하므로, 총 복잡도는 $O(n)$이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 5e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int id[MAXN];
int mxv[MAXN];
int dp[MAXN];
int psum[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>x;
        id[x] = i;
        A[i] = x;
    }

    for(int i=1;i<=n;i++){
        mxv[i] = max(mxv[i-1],A[i]);
    }

    dp[0] = 1;
    psum[0] = 1;

    for(int i=1;i<=n;i++){
        mx = mxv[i];
        idx = id[mx];

        dp[i] = psum[idx-1];

        psum[i] = psum[i-1]+dp[i];

        if(psum[i]>=MOD)psum[i]-=MOD;
    }

    cout<<dp[n]<<"\n";


    return 0;
}

여담: 블로그 글 처음에는 연습 이미지 순서가 잘못 돼 있었는데, jwvg0425님의 도움으로 빠르게 고칠 수 있었다. thanks in advance.