ICPC 2021 예선 후기 및 풀이

작성일 | In |

들어가기 전에

ICPC 예선은 UCPC와 완전히 동일한 팀원으로 진행했다. 이미 UCPC 예선 후기글에서 간단히 언급했지만, 다시 한번 정리하자면

cs71107(CF,BOJ, 블로그 주인장) sait2000(CF,BOJ) IHHI(CF,BOJ)

이렇게 세 명으로 구성 돼있다.

팀명은 눈치 챌 사람은 눈치 챘겠지만, 각 멤버 핸들의 첫 글자를 따서 CSI 로 결정했다. 팀명은 내가 정했는데, 이렇다할 아이디어가 없어서 그냥 첫 글자 딴 CSI로 하자! 고 하니까 멤버들이 동의해서 결정됐다.

서울대의 경우, ICPC Regional 진출 여부를 문제 수로 컷하는 경우가 많았다. 만약 3~7위가 모두 동일한 수의 문제를 푸는 경우 (서울대의 경우 휴학생팀 제외 이번 대회에 총 12팀이 참가했다.) 3위도 자칫하면 떨어질 수 있다는 생각을 했다. 하지만 UCPC에서는 아주 좋은 결과를 내었기 때문에, UCPC 가 끝나고 나서 우리 팀 정도면 Regional에 갈 수 있지 않을까? 하는 생각을 하면서 준비했다.

대회 준비 과정

ICPC의 경우 UCPC와 달리 1컴으로 문제를 풀어야 하기 때문에, 지금까지와 달리 1컴으로 문제를 푸는 연습이 필요했다. 나의 경우 작년에 ICPC 참가 경험이 있기 때문에, 3컴, 1컴 차이가 얼마나 큰지 알고 있었고, 1컴으로 연습들을 진행하고자 했다.

ICPC 예선 연습을 총 3번 진행했는데, 첫번째, 두번째는 디스코드를 통해서 소통하며 3컴으로 진행했다. (디스코드를 통해 컴퓨터를 잡고 싶은 사람이 말하고, 특정시간대에는 한 사람만 키보드를 건드릴 수 있는 방식) 세번째는 직접 만나서 UCPC를 진행했던 slab이란 곳에서 진행했다.

첫번째 연습의 경우 2018 Jakarta Regional, 두 번째 연습은 GCPC 2018, 세 번째 연습은 NCPC 2019로 진행했다. 세번째 부터는 직접 만나서 진행했던 만큼, csi2021이라는 계정을 따로 파서 진행했다.

각 연습의 결과를 첨부한다.

2018 Jakarta Regional:

GCPC 2018:

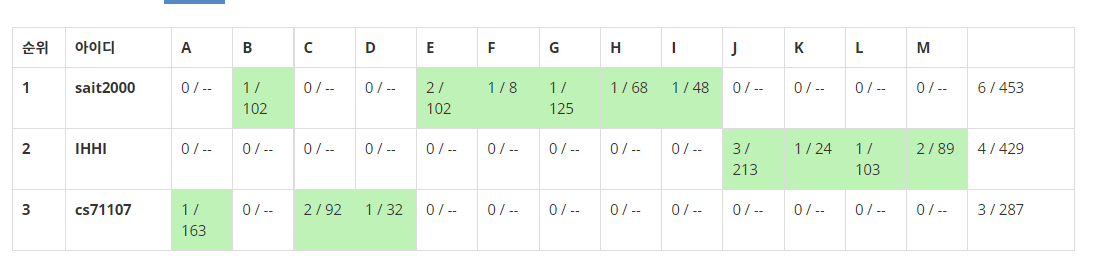
NCPC 2019:

연습 결과를 보면 알겠지만, solved.ac 기준으로 다이아 이상의 문제를 밀지 못했다는 것을 알 수 있다. 하지만 플1을 포함한 플레 이하의 난이도는 확실히 밀어주는 모습을 보여주었기 때문에, 예선을 통과할 수 있을 거란 기대를 가졌다.

연습 때 프린트 문제가 이슈로 지적돼서 (원랜 동아리 방에서 출력이 가능했는데, 그날 이슈가 있어 프린트 문제 때문에 연습이 매우 지연되는 사태가 있었다.), 프린트가 가능한 스터디 카페를 물색하던 중, 서울대 입구 주변의 토즈 모임센터에서 진행하기로 결정했다. 프린트는 Sait님이 프린터기를 직접 가져오는(!) 것으로 해결.

대회 전날 Sait님과 함께 환경 점검 및 예비소집을 거치고 밥을 먹었다.

그 외에 팀노트의 경우 더불어민규당의 팀노트를 가져오고, 거기다가 센트로이드, 샤모스-호이 등 여러 가지 우리가 필요한 것들을 추가하고, 우리가 필요 없는 (general matching 가중치 있는 버전) 같은 것들을 제외시켰다.

팀노트에 있는 알고리즘들을 쓰는 문제들을 개인적으로 풀 수 있는 문제들을 그룹에 만들어두긴 했으나, 그다지 효과가 있었던 것 같지는 않다.

대회 진행 과정

14:00~ - 대회시작, 문제지가 통합돼있는 파일을 찾았으나 찾을 수가 없어서, 일단 급한 대로 각 문제들마다 뽑기로 하고 문제를 뽑기 시작했다. 이때 프린트 이슈 발생, 나중에서야 통합 파일이 올라온 것을 발견했다. 문제가 총 12문제였기에, 평소대로 ABCD가 나, EFGH는 Sait님, IJKL은 IHHI 가 맡아서 문제를 읽기 시작했다.

14:11 - IHHI가 I를 읽더니 이게 등록 문제 급이네요 ㅇㅇ 하더니 짜서 맞았다.

14:21 - 내가 A를 읽고 넘긴 후 B를 읽고 Sait신에게 넘기고 있을 때, IHHI가 J도 이렇게 하면 될 것 같다면서 열심히 짜고 제출했으나 결과는 WA, 디버깅 하더니 무슨 실수인지 알았다면서 고쳐서 바로 AC.

14:32 - B의 경우, 수학 스런 느낌이 나는 case work 문제였고, 처음엔 내가 풀 수 있을 줄 알고 덤볐으나 케이스가 있다는 걸 깨닫고 이런 걸 우리 팀에서 제일 잘하시는 Sait신에게 토스, Sait신에게 문제 설명과 약간의 대화를 거친 후, Sait신이 열심히 풀이 구체 및 구현을 마치고 AC. (B 퍼솔!)

이 시점에서 스코어보드 상 우리가 1위였다.

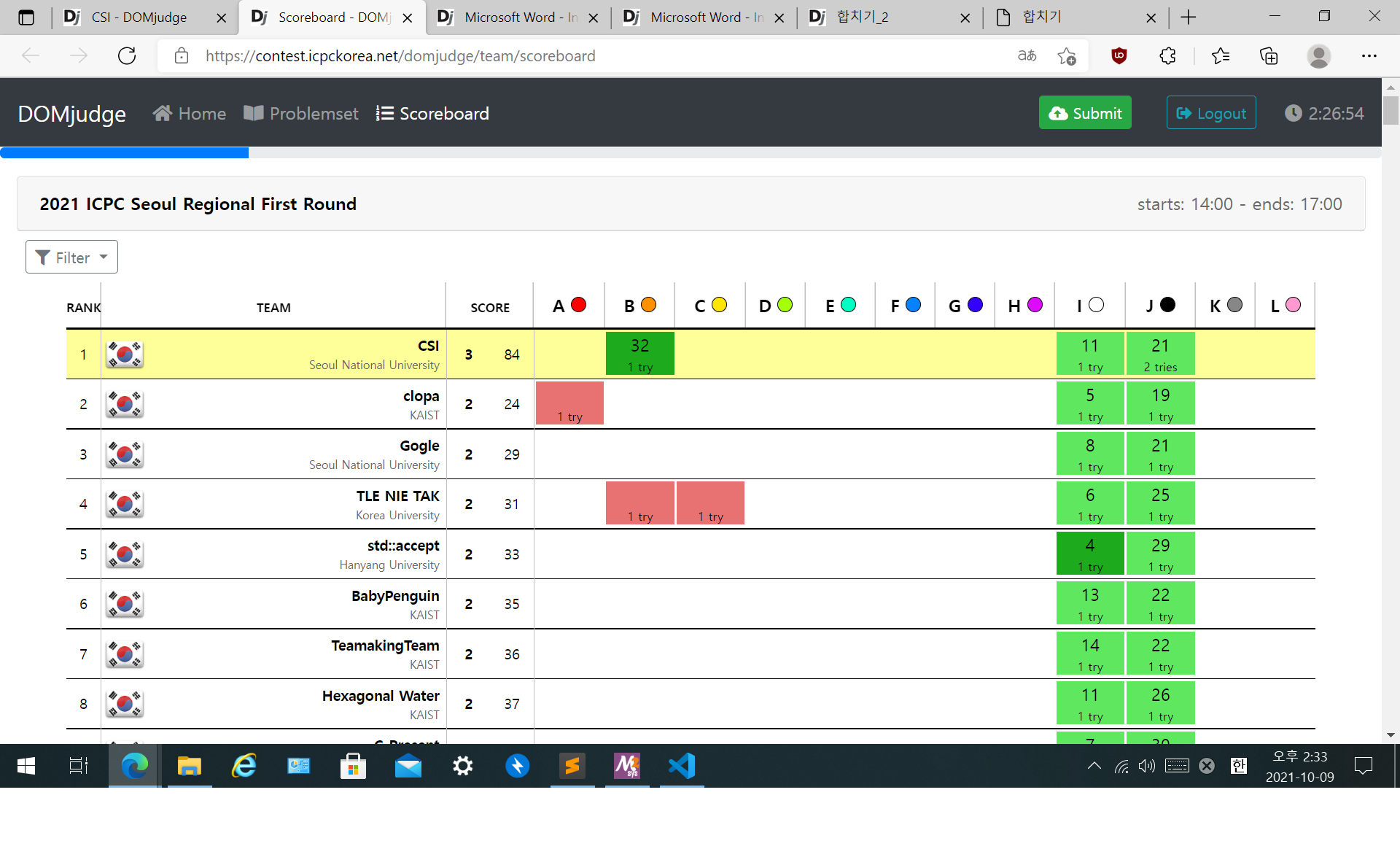
여기까지 온 이후, C의 경우 난 풀이가 잘 생각이 안 나서 일단 넘긴 상태였고, D를 잡아보려고 한 상태였다.

14:54 - 스코어보드를 보니, H, E가 풀린 상태여서 보니 H가 IDT나 segtree를 사용하면 쉽게 풀리는 문제여서, 내가 잡았다. IDT를 통해서 빠르게 구현하고 예제가 나오는 것을 확인후, 제출. AC.

15:20 - 내가 H를 열심히 풀 동안 Sait과 IHHI는 C를 잡고 고민하고 있었다. C의 풀이를 대략적으로 알아냈고, 내가 H를 푼 후 제출했으나 WA. 나와 IHHI가 디버깅에 들어갔고, Sait신은 E를 잡았다. C의 케이스 처리 두 개를 못해준 것을 제출 하나당 발견해서, 2틀 후 AC.

15:30 - Sait신이 E의 입력 크기를 통해 추론한 dp풀이가 정당하다고 판단해서 코딩했으나, 결과는 예제 컷이 나왔다. 공식 사용도 완벽했기 때문에, 뭐가 문제인지 알 수 없었는데, 내가 Sait신이 실수 나눗셈을 해야 하는데 정수 나눗셈을 한 것을 발견했다. (파이썬에 익숙하신 나머지 정수 나눗셈은 //, 그냥 나눗셈을 /로 생각해서 발견하기 힘들었던 것) 그리고 그 부분을 고친 후 예제가 통과하는 것을 발견. 제출 후 AC.

Sait신이 E를 해결할 동안, 나와 IHHI는 L을 고민했고, 크기상 이정도면 O(n^3)이 돌지 않을까? 라고 생각하면서 풀이를 찾아냈고, IHHI가 L을 구현하는 동안 나와 Sait신은 A를 고민했으나, 잘 풀리지 않고 있었다.

L에서 IHHI의 구현이 예제가 잘 나왔으나 AC를 받지 못했고, 당연히 WA일 것이라 생각한 우리는 신나게 디버깅을 하고 있었다. 하지만 도저히 WA 원인을 찾을 수가 없었고, 그때 Sait신은 자신의 A 풀이를 구현하고 있었으나 맞을 거라는 확신이 없는 상태였다. 풀린 문제 중 우리가 못 푼 문제가 A,K,L 정도였기 때문에, L의 디버깅을 잠시 쉬고 K를 봤으나 역시 유의미한 성과는 없었다.

15:43 - K 풀이를 나와 Sait신이 열심히 토론하던 중에, IHHI가 이렇게 하면 안 되냐고 해서 K를 구현하고 제출했으나, (대충 세그트리를 쓰는 풀이였던 걸로 기억한다.) WA를 받았다. 이대로 6솔로 끝나는 건가? 싶던 중…

IHHI가 제출 내역을 보더니 K결과가 WA가 아니라 TLE(….) 라는 소식을 전했다. 대회 종료 17분이 남은 시점에서, 우리는 급히 L 풀이의 복잡도를 끌어내리는 작업에 들어갔다. Sait신과 IHHI가 동시에 달라붙어서 코딩에 들어갔고, 나는 A,K 를 다시 한번 보고 있었다.

15:55 - 제출한 코드가 예제컷 나는 광경을 지켜보면서 가슴이 철렁하는 경험을 몇 번 하고, (상황이 급박해서 난 예전 코드에 pragma gcc를 박은 코드라도 제출해보자는 의견도 냈었다.) 드디어 예제가 나오는 코드가 완성 됐다. 그리고 떨리는 마음으로 제출… 그리고 그 코드는 AC를 받았다! 그렇게 우리는 종료 5분전에(…) 7솔을 달성할 수 있었다.

대회 결과

대회가 끝나고 나서 전체 순위는 그리 나쁘지 않을 것으로 예상됐지만, 서울대 내 순위가 중요했기 때문에 수소문한 결과, 내가 얘기했던 대로 서울대 내 3~7위 팀이 전부 7솔이라는 사실을 알아챘다.

그전까지 서울대는 문제 수로 컷을 냈기에 최악의 경우 이번에도 예선 탈락을 경험할 수 있을 것이란 불안감을 가지고 밥을 먹으러 갔다.

스코어보드가 나오자 서울대 내 3위라는 것을 알게 됐고, 웬만하면 진출할 것이라고 생각했다.

그 후 본선팀 발표에서 문제 수 컷이 6솔로 확정됐고, 서울대는 우리 팀을 포함해 총 7팀이 진출이 확정됐다.

당시 스코어보드

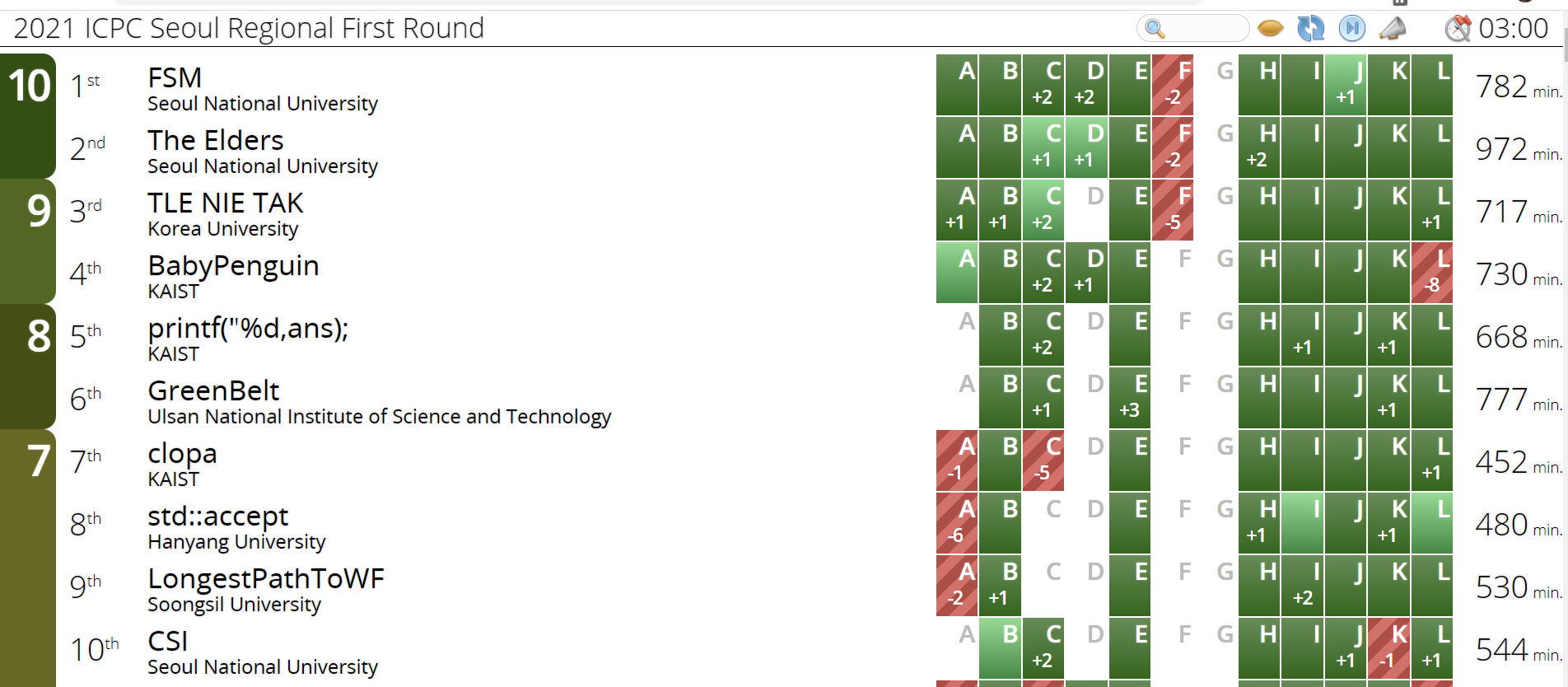
전체 스코어보드는 여기에서 확인 가능하다.

총평

여러 모로 아쉬움이 많이 남는 대회였다. 우선, TLE를 WA로 착각하여 의미없는 데에 상당한 시간을 낭비했다. 또한, 연습 때와 마찬가지로 여전히 solved.ac 기준 다이아 급의 문제를 밀지 못했다.

K의 경우 난이도를 볼 때 우리 팀 정도면 충분히 밀 수 있었던 문제로 보이나, L에 집중해야 했고 & 거기다가 약간 발상 단계에서 말리는 바람에 풀지 못했다.

A의 경우 그냥 아이디어를 떠올릴 시간이 부족했던 것으로 보인다.

프린트 이슈부터 시작해서 여러모로 아쉬운 점이 많은 대회였다.

문제 풀이

UCPC 후기 처럼 내가 풀이를 갖고 있는 문제들에 한해서 서술한다. 업솔빙을 진행함에 따라 여기에 풀이가 추가될 수 있음.

전체 문제에 대한 풀이는 구사과님의 블로그 글에 나와있으니 참고하기 바란다.

A. Best student

대회 중엔 풀지 못했던 문제,

구간이 여러 개 주어지고, 해당 구간내에 가장 자주 등장한 값 중에서, 가장 큰 값을 출력해야 한다.

아마 이 글을 읽는 사람들이라면 아마 대부분 수열과 쿼리문제들을 떠올릴 것이다.

일단 업데이트가 없고, 뭔가 세그 트리로 처리하긴 어려워 보이니 Mo’s Algorithm을 써야 하긴 할 것 같아 보인다.

하지만 그냥 구간에 대해서 bucket을 나누어선 풀기 어렵다. 나도 들은 풀이지만, 내가 접근한 방법은

바로 수들에 대해서도 구간을 나누는 것이다. 현재 배열 내에 서로 다른 수가 많아봤자 $N$개가 있으니, $\sqrt(N)$개로 버킷을 나눈 후, 각각의 버킷에 대해 속하는 수들에 대해 가장 자주 등장하는 수가 현재 몇 번 등장하는지를 관리해준다.

그렇게 업데이트를 진행하면, 큰 수들이 속하는 버킷부터 훑으면서 전체에서 정답이 속하는 버킷이 어디인지 찾고 (이 과정에서 $O(\sqrt(N))$)가 걸린다. 그리고 그 버킷 내에서 다시 정답을 찾는다. (다시 $O(\sqrt(N))$)이 걸린다.) 이렇게 하면 총 시간 복잡도

$O((N+Q)\sqrt(N))$에 풀수가 있다. 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
pii query[MAXN];
vector<pii> qq[330];

int cal[2*MAXN];
int vv[330];
int ccal[330][MAXN];

int ans[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1,idy = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>q;

    vector<int> pos;

    for(int i=0;i<n;i++){
        cin>>A[i];
        pos.push_back(A[i]);
    }

    const int sqn = (int)sqrt(n);

    for(int i=0;i<q;i++){
        cin>>a>>b;
        query[i] = pii(a-1,b-1);
        qq[(a-1)/sqn].push_back(pii(b-1,i));
    }

    sort(pos.begin(),pos.end());
    pos.erase(unique(pos.begin(),pos.end()),pos.end());

    m = (int)pos.size();

    const int sq = (int)sqrt(m);

    for(int i=0;i<n;i++){
        A[i] = lower_bound(pos.begin(),pos.end(),A[i])-pos.begin();
    }

    const int esq = (n-1)/sqn;

    for(int i=0;i<=esq;i++){
        sort(qq[i].begin(),qq[i].end());
    }

    const int msq = (m-1)/sq;

    for(int i=0;i<=msq;i++){
        ccal[i][0] = sq;
    }

    cur = A[0];

    a = cur/sq;

    cal[cur] = 1;

    ccal[a][0]--;
    ccal[a][1]++;

    vv[a] = 1;

    int st = 0,en = 0;

    for(int i=0;i<=esq;i++){

        const int cursz = (int)qq[i].size();

        for(int j=0;j<cursz;j++){

            idx = qq[i][j].s;

            x = query[idx].f;
            y = query[idx].s;

            for(int t=st-1;t>=x;t--){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]++;

                ccal[a][cnt]--;
                ccal[a][cnt+1]++;

                if(!(vv[a]^cnt)){
                    vv[a]++;
                }
            }

            for(int t=en+1;t<=y;t++){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]++;

                ccal[a][cnt]--;
                ccal[a][cnt+1]++;

                if(!(vv[a]^cnt)){
                    vv[a]++;
                }
            }

            for(int t=st;t<x;t++){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]--;

                ccal[a][cnt]--;
                ccal[a][cnt-1]++;

                if((!ccal[a][cnt])&&(!(cnt^vv[a]))){
                    vv[a]--;
                }
            }

            for(int t=en;t>y;t--){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]--;

                ccal[a][cnt]--;
                ccal[a][cnt-1]++;

                if((!ccal[a][cnt])&&(!(cnt^vv[a]))){
                    vv[a]--;
                }
            }

            st = x;
            en = y;

            mx = 0;
            idy = -1;

            for(int t=msq;t>=0;t--){
                if(mx<vv[t]){
                    mx = vv[t];
                    idy = t;
                }
            }

            assert(mx>0);

            cur = idy*sq;

            for(int t=cur+sq-1;t>=cur;t--){
                if(cal[t]^mx)continue;
                ans[idx] = t;
                break;
            }
        }
    }


    for(int i=0;i<q;i++){
        cur = ans[i];
        cout<<pos[cur]<<"\n";
    }


    return 0;
}

H. Similarity

결국 두 수열 $p, q$에 대해서, $p_{i} < p_{j} < p_{k} $이고 $q_{i} < q{j} < q_{k}$인 $i,j,k의 개수를 세라는 것이므로,

저 위의 조건에서 $j$ 기준으로 생각하면, 결국 답은

각각의 $j$에 대해서, 가능한 $i$의 개수와 $k$의 개수를 곱한 것을 전부 더한 값이다.

그리고 $j$에 대한 $i$의 개수는 $p_{i} < p_{j}$이고 $q_{i} < q_{j}$인 개수를 세는 것인데, 이는 널리 알려져 있다 시피 segment tree등을 활용하면 쉽게 셀 수 있다.

비슷하게 $j$에 대한 $k$의 개수도 셀 수 있다.

코드는 다음과 같다. 복잡도는 $O(NlogN)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>
#define f first
#define s second
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
const int MAXN = 2e5+10;
const int MAXNN = 1e6+10;
pii A[MAXN];

vector<int> pp[MAXNN];
int tree[MAXNN*4];

int Lv[MAXN];
int Rv[MAXN];

inline void update(int tmp){

    while(tmp){
        tree[tmp]++;
        tmp>>=1;
    }
    return;
}

inline int getans(int L,int R){
    int res = 0;
    while(L<=R){
        if(L&1){
            res += tree[L];
            L++;
        }
        if(!(R&1)){
            res += tree[R];
            R--;
        }
        L>>=1; R>>=1;
    }
    return res;
}

int main(){

    int n;
    int mx = 0;
    int my = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(0);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>A[i].f;
        mx = max(mx,A[i].f);
    }

    for(int i=1;i<=n;i++){
        cin>>A[i].s;
        my = max(my,A[i].s);
    }

    for(int i=1;i<=n;i++){
        pp[A[i].f].push_back(i);
    }

    int base = 1;

    for(;base<=my;base<<=1);

    int cursz = 0;
    int idx = 0;

    for(int i=0;i<=mx;i++){
        cursz = (int)pp[i].size();

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            Lv[idx] = getans(base,base+A[idx].s-1);
        }

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            update(base+A[idx].s);
        }
    }

    fill(tree,tree+MAXNN*4,0);

    for(int i=mx;i>=0;i--){
        cursz = (int)pp[i].size();

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            Rv[idx] = getans(base+A[idx].s+1,base+my);
        }

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            update(base+A[idx].s);
        }
    }

    ll res = 0;

    for(int i=1;i<=n;i++){
        res += (1LL*Lv[i]*Rv[i]);
    }

    cout<<res<<"\n";

    return 0;
}

I. Sport Climbing Combined

그냥 정렬 기준을 세워서 함수를 짠 다음 정렬 시켜주면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

struct P{
    int va,vb,vc;
};

bool cmp(const P&p,const P&q){
    if(!(p.va^q.va)){
        if(!(p.vb^q.vb))return p.vc<q.vc;
        else return p.vb<q.vb;
    }
    else {
        return p.va<q.va;
    }
}

P A[110];

int main()
{
    int n,m,k,a,b,c,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>k>>a>>b>>c;
        A[i] = {a*b*c,a+b+c,k};
    }

    sort(A+1,A+n+1,cmp);

    for(int i=1;i<=3;i++){
        cout<<A[i].vc<<" ";
    }
    cout<<"\n";

    return 0;
}

J. Ten

여러 가지 방법이 있겠으나, 현재 제한 조건 상 각 셀의 수는 반드시 양의 정수이고, 정확히 10인 것만 세면 되므로, 후보로 가능한 직사각형의 넓이는 10을 넘을 수 없다.

따라서 오른쪽 아래 점 후보로 가능한 모든 점을 순회하면서 후보 직사각형 (넓이가 10이하)인 것들을 모두 확인하는 것으로도 충분히 시간안에 돌아간다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[510][510];
int psum[510][510];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>A[i][j];
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            psum[i][j] = A[i][j]+psum[i-1][j]+psum[i][j-1]-psum[i-1][j-1];
        }
    }

    int res = 0;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){

            for(int t=1;t<=10;t++){

                if(i<t)break;

                idx = min(10/t,j);

                for(int tt=1;tt<=idx;tt++){
                    cur = psum[i][j]-psum[i-t][j]-psum[i][j-tt]+psum[i-t][j-tt];
                    if(cur==10)res++;
                }
            }
        }
    }

    cout<<res<<"\n";

    return 0;
}

K. Treasure Hunter

대회 중에 못 풀었던 문제로, 우리 팀의 수준이라면 풀 수 있었을 텐데 하고 아쉬움이 남는 문제이다. 아마 대회 당시엔 말렸던 것 같다.

문제에서 원하는 것은 결국 (증명은 아직 잘 모르겠지만) LIS로 환원시킬 수 있고, 좌표를 적절하게 변환한 후 LIS를 구해주면 된다.

복잡도는 $O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

vector<int> id[MAXN];

int val[MAXN];
int tree[MAXN*4];

int getans(int L,int R)
{
    int res = 0;
    while(L<=R){
        if(L&1){
            res = max(res,tree[L]);
            L++;
        }
        if(!(R&1)){
            res = max(res,tree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }
    return res;
}

void update(int tmp,int v)
{
    while(tmp){
        tree[tmp] = max(tree[tmp],v);
        tmp>>=1;
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m>>k;

    for(int i=1;i<=k;i++){
        cin>>y>>x;
        y = n-y;
        id[x].push_back(y);
    }

    int base = 1;
    for(;base<n;base<<=1);

    for(int i=1;i<=m;i++){

        for(int j=0;j<(int)id[i].size();j++){
            idx = id[i][j];
            cur = getans(base,base+idx-1)+1;

            val[j] = cur;
        }

        for(int j=0;j<(int)id[i].size();j++){
            idx = id[i][j];
            update(base+idx,val[j]);
        }
    }

    cout<<tree[1]<<"\n";


    return 0;
}