작성일 | In |

들어가기 전에

ICPC 예선결과가 나오고 나서, 일단은 각자 할일이 있었기 때문에, 각자 할일을 하면서 ICPC 본선을 준비하게 됐다.

대회 준비 과정

ICPC 예선 연습처럼, 본선 역시 csi2021이라는 계정을 통해서 연습을 했다.

연습 장소는 ICPC 본선을 칠 스터디 카페에서 해보면 제일 좋겠지만, 시간과 비용의 문제로 그냥 서울대 윗공대 slab의 방 하나와, 컴퓨터공학부 과방에서 연습을 진행했다.

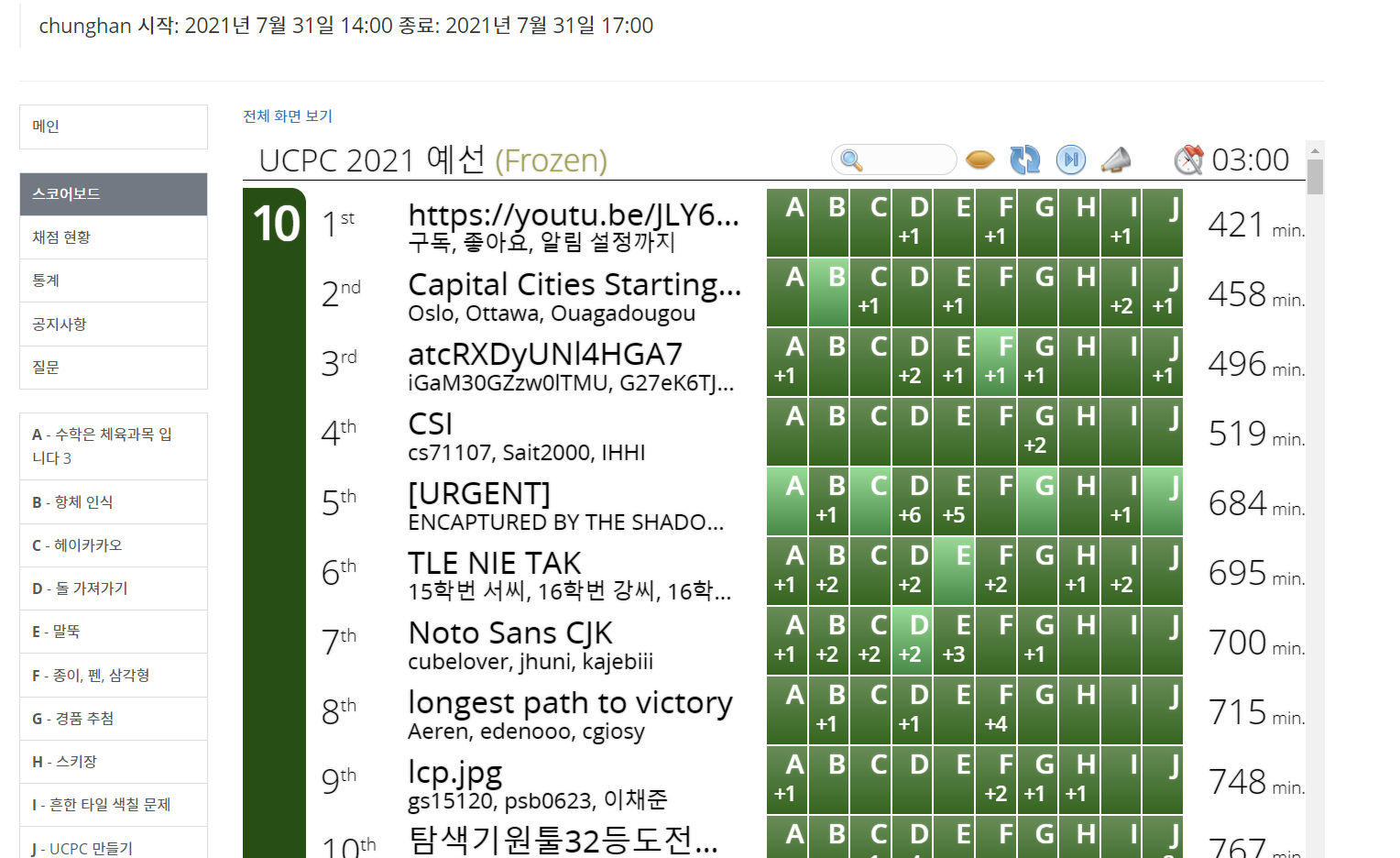
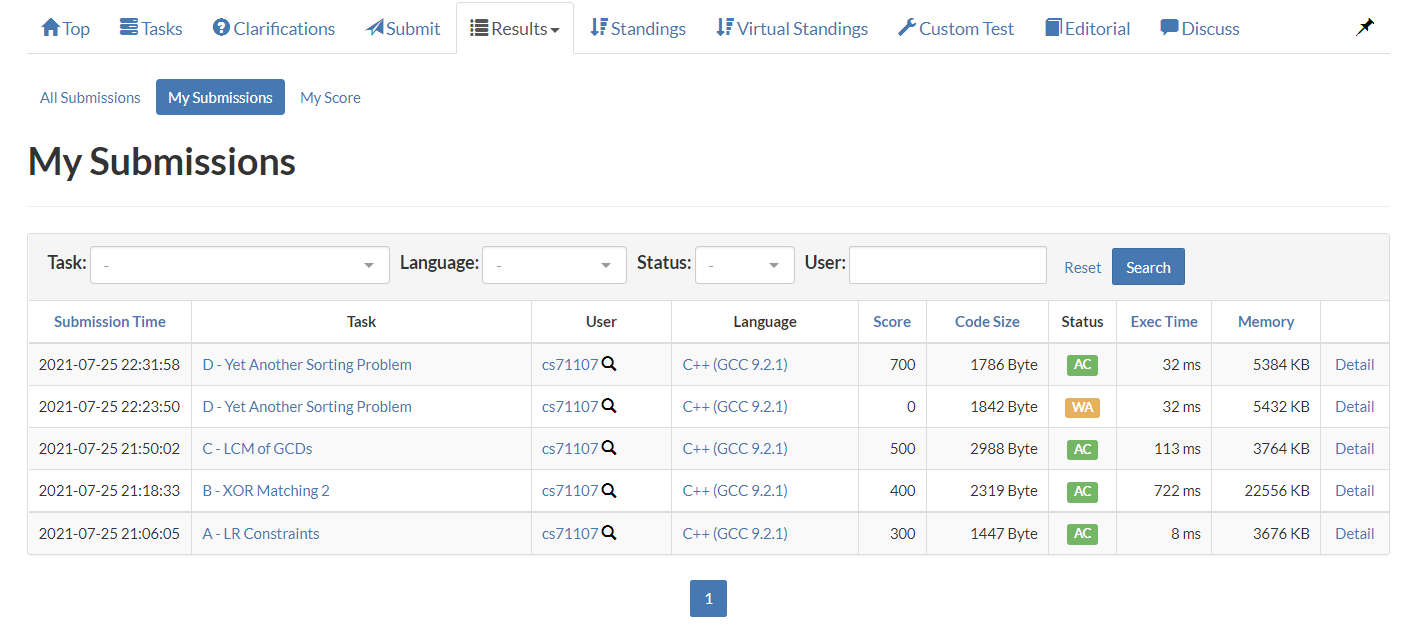
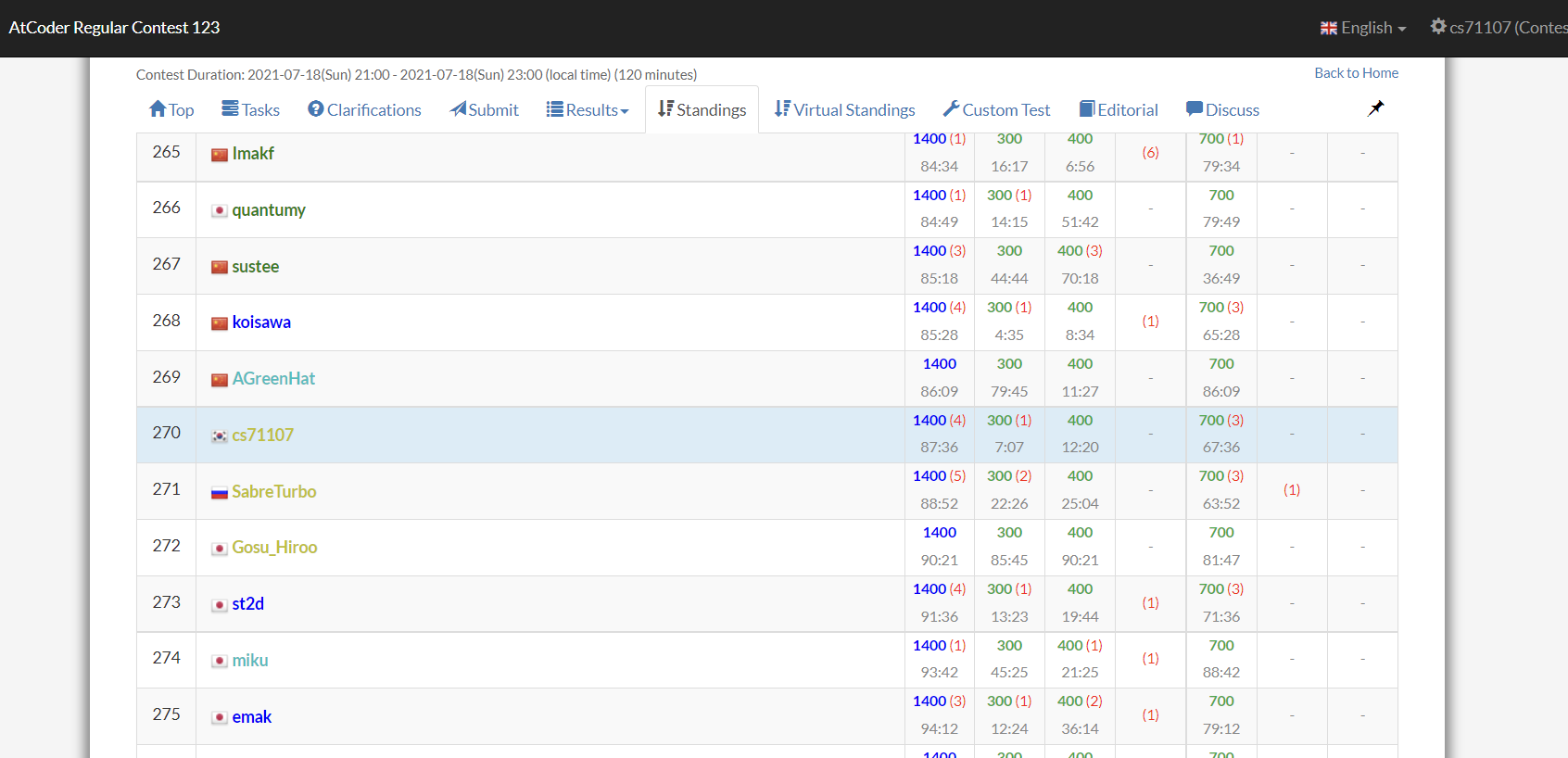
첫번째 연습의 경우 2020 Asia Yokohama Regional, 두번째 연습의 경우 Latin America Regional Contests 2019을 사용해서 연습을 진행했다.

각 연습의 결과를 첨부한다.

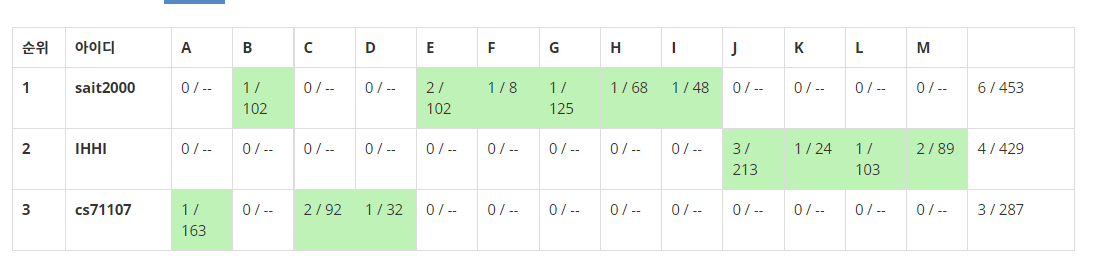
2020 Asia Yokohama Regional:

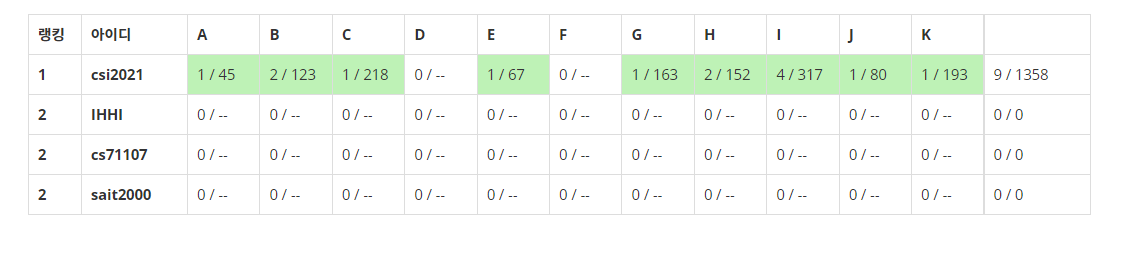
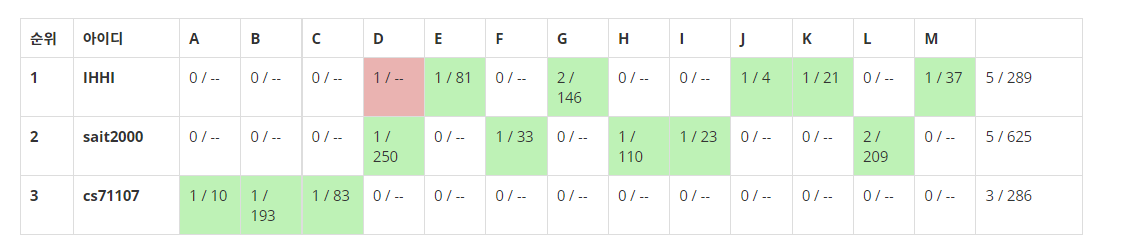
Latin America Regional Contests 2019:

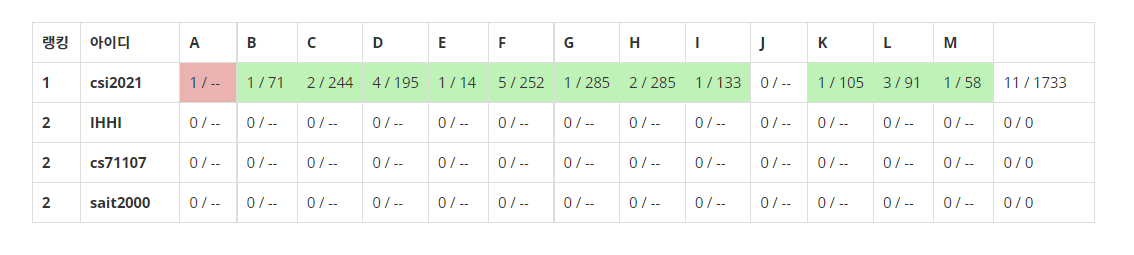
2020 Asia Yokohama의 경우 LCM of GCDs란 문제가 예전에 Sait님에 의해 풀려 있었는데, 내가 그걸 체크하지 않은 상태로 연습에 돌입했었다. 단, Sait신도 명확하게 어떤 문제였는진 당시에 기억하지 못했다.

Latin 2019의 경우 Sait신이 연습 중에 라이브로 DB를 박아서 다이아를 푸는 것을 목격했다. Sait신….

보다 시피 연습 결과가 상당히 좋았다. 두 연습 모두 2개 정도의 문제를 제외하면 모두 풀었고, 하위 다이아 문제도 푸는데 성공했음을 볼 수 있다. 그래서 연습 과정에서 어느 정도 자신감을 얻은 상태로 ICPC 본선에 들어갔다.

본선을 친 장소는 예선과 똑같은 서울대 입구 주변의 토즈 모임센터에서 진행하기로 결정했다. 프린터기는 여전히 Sait님의 운반하시기로 했다.

대회 전에 ICPC 본선용 키트 (스웨트, 현수막 등등)이 도착했고, 난 ICPC 스웨트를 입고 서울대 입구에 나갔다. 거기에서 팀원들과 합류한 이후, 먼저 스터디 카페에 짐을 풀었다. 그리고 근처에 KFC가 있어 간단하게 요기를 했고, 현수막, 노트북, 프린터기 등 대회 준비를 위한 기본 환경 설정을 마쳤다. 대회 시작 전에, 긴장을 풀기 위해서 잡담을 좀 나눴는데, 우리끼리는 한 5위 정도 하면 우린 성공인 것 같다고 얘기를 했다. 아래 부터는 실제 대회 내 진행과정이다.

대회 진행 과정

12:00~ - 대회시작, 일단 문제지를 뽑았고, 평소대로 내가 ABCD, Sait님이 EFGH, IHHI가 JIKL을 맡았고, 문제들을 읽기 시작했다.

12:10~20 - 우선 A가 어려운 트리 문제(시간을 들여야 하는 타입)이라는 걸 깨닫고 넘겼고, B를 보니 전형적인 문제라서, 짤 수 있겠다는 생각이 들어서 빠르게 구현해서 바로 AC를 맞았다. B 솔브.

12:24~ - 그 사이에 IHHI가 C를 풀어서 구현, 바로 AC를 맞았다. 그때 난 D를 읽고 있었다. D를 읽으니 풀 수 있겠다는 감이 왔고, 구현을 시작했다. C 솔브.

12:44 - 열심히 짰으나…. 결과는 WA. 그 순간 나는 멘붕이 왔고, 일단 프린트를 해서 디버깅을 하기로 결정했다.

12:58 - 내가 열심히 디버깅을 하고 있을 때, F의 풀이를 알아낸 Sait신이 빠르게 구현을 해서 AC를 받았다. 그리고 난 내 구현의 방향성이 살짝 잘못됐다는 걸 깨닫고, Sait신이 AC를 받자마자 바로 구현을 시작했다. F 솔브.

13:03~13:09 - D를 제출했으나, 또 틀렸다… 다시 멘붕이 왔고, 우리팀의 페널티는 나 혼자 만들어내고 있는 상황이었다. 다시 출력 후 디버깅에 들어갔다. 그리고 정말 어이 없는 구현 실수로 WA를 받았음을 깨달았다. 빠르게 고치고 다시 냈고, 마침내 AC! D 솔브.

13:10~41 - 그사이에 IHHI가 L의 풀이를 알아냈고, 열심히 구현을 하기 시작했다. IHHI가 열심히 구현한 L을 제출했고… 결과는 AC! L 솔브.

13:41~58 - IHHI가 L을 구현하고, 난 다른 문제를 읽고 있는 동안에, Sait신이 K가 SCPC 때 나왔던 바로 그 유형이라면서 L의 결과가 나오자마자 열심히 코딩을 하기 시작했다. 팀노트에 있는 KMP구현 등등을 살짝 뒤지고 구현을 마친 후, 제출했더니 결과는 AC. K 솔브.

13:58~14:12 - Sait신이 K를 열심히 구현할 때, 나와 IHHI는 G의 풀이를 의논하고 있었다. 내가 G와 비슷한 문제를 코포에서 만났던 기억이 있기 때문에, 왠지 dfs+dp일 것 같다라는 의견을 말했고, IHHI도 풀이를 확신해서 바로 구현에 들어갔다. 난 그때 아주 강한 확신은 없었지만, 어쨌거나 IHHI는 구현을 마쳤고, 바로 AC를 맞았다. G 솔브.

14:12~14:34 - 우리가 G에 신경 쓰고 있을 동안, 우리는 E가 수학이라는 것을 파악하고 Sait신에게 토스를 한 상황이었다. Sait신이 뭔가를 열심히 뚝딱뚝딱하고, 우리에게 의견을 구했다. 우리가 맞는 것 같다고 하자 Sait신이 E 구현에 들어갔고, AC를 받았다. E 솔브.

이 시점에서 스코어보드를 확인했고, 현재 전체 2위, 서울대 1위임을 확인했다.

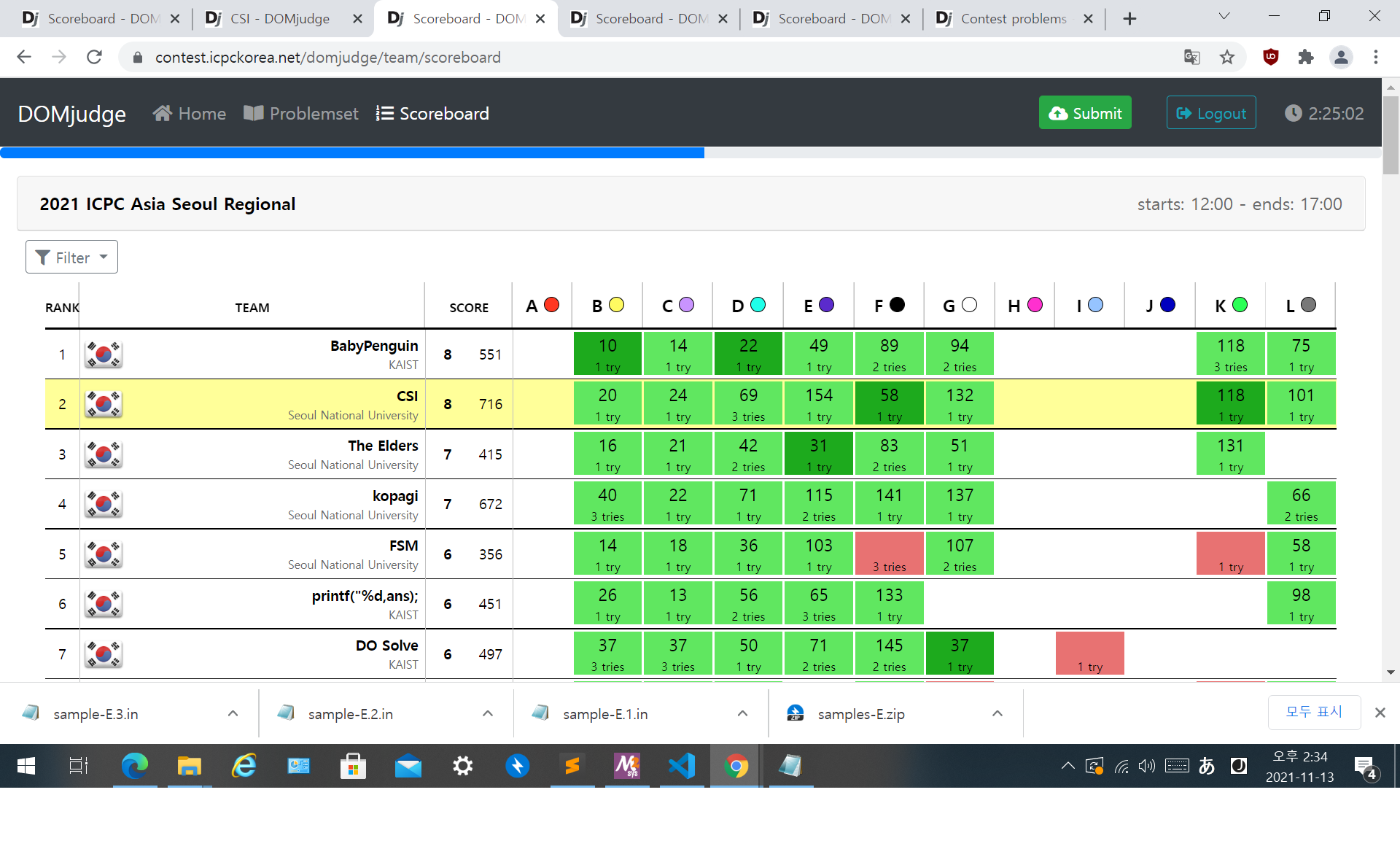
스코어 보드를 확인한 결과, 문제가 4개 남았기 때문에 각자 한 문제씩 잡고 남은 시간을 보내는 것으로 했다. H가 많이 어려워 보였기 때문에, 일단 H를 제외하고, 트리+자구스런 문제인 A를 내가, I를 IHHI가, J를 Sait님이 이렇게 나누었다.

14:34~16:09 - A의 풀이를 열심히 고민한 결과, HLD+세그먼트 트리를 쓰면 문제를 풀 수 있다는 결론을 도출했다. 단, 풀이에서 쓰는 주요 알고리즘만 봐도 느껴지듯이, 적어도 나에겐 굉장한 구현량을 요구하는 문제였다. 그렇게 때문에 일단 다른 문제 중 풀이가 나온 것이 있으면 바로 교체할 수 있도록 하되, 일단 A 구현을 시작했다. A는 굵직한 풀이도 구현이 많이 필요하지만, 디테일한 처리도 필요한 문제였다. 그렇게 1차적으로 구현을 마치고 나자, 400줄이 넘는 구현이 나왔고… 디버깅도 힘들겠다 판단해서 예제가 나오는 걸 보자 그냥 바로 냈다. 결과는 WA….

16:09~ - 이제 시간이 1시간도 남지 않아서, A가 WA가 뜨자 모두 A 디버깅에 달려 들었다. 하지만 내 코드가 워낙 길고 + 나만 쓰는 특징들이 있던터라 같이 디버깅하기가 힘들었다. 그 뒤로 내가 잘못 구현한 것들을 하나씩 찾아냈고, 그때마다 제출해보았으나 WA 2번을 더 쌓는… 결과만 낳았다.

16:52~ - 최후의 수단으로 작은 입력을 몇 개 만들어서 잘못된 답을 내는 입력이 있는지 찾아보기 시작했고, 운이 좋게도 해당 입력을 얼마 지나지 않아 찾을 수 있었다. 그리고 내가 정말 바보 같은 실수를 했다는 걸 깨달았다. 해당하는 오류를 빠르게 고쳤고, 지금까지 만들었던 입력 + 예제들을 모두 넣어본 후, 제대로 결과가 나오는 것을 확인했고, 제출한 뒤… AC. 결국 종료 8분 전에야 A를 맞을 수 있었다. 그 뒤 남은 문제는 I,J가 있었는데 사실상 풀이를 찾지 못해서 이대로 대회를 마쳤다.

대회 결과

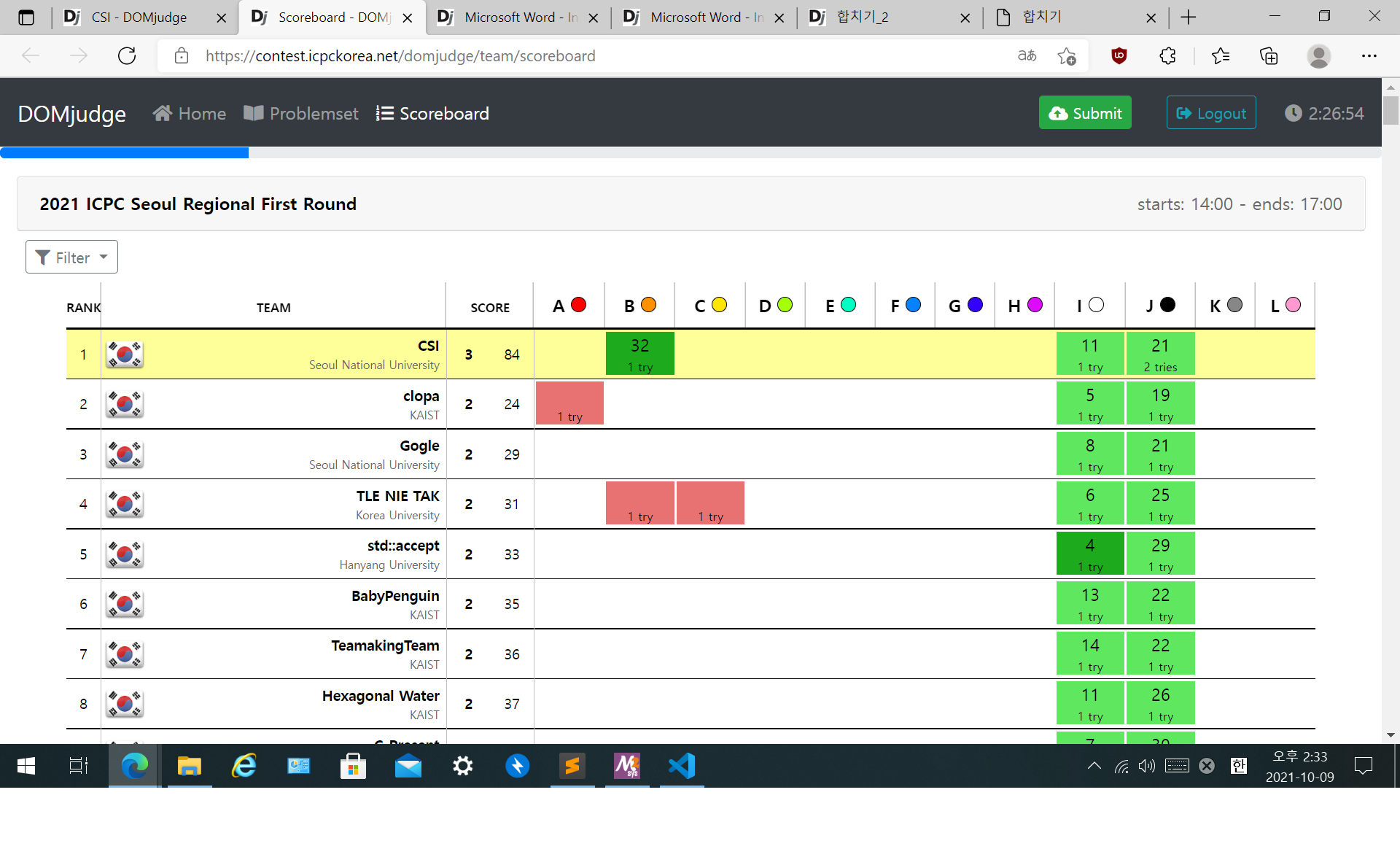
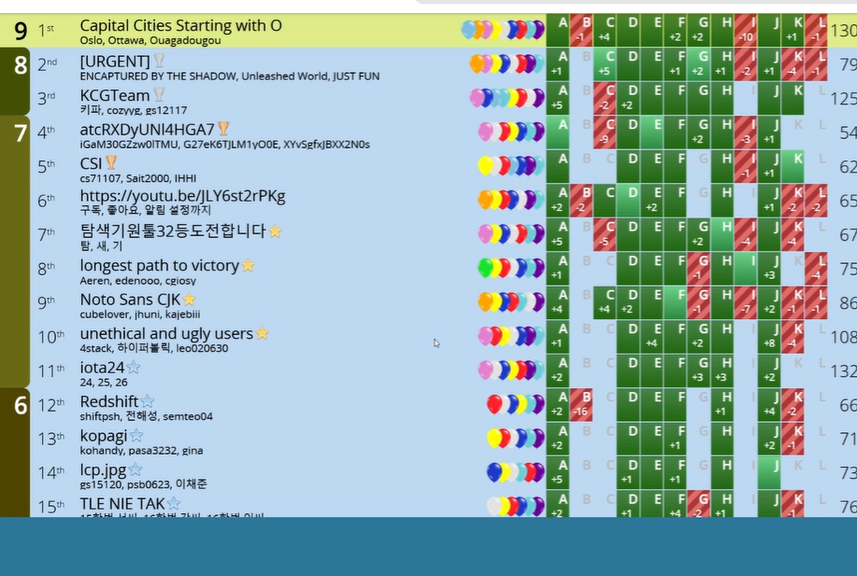
대회가 끝나기전에 캡처한, 프리즈가 풀리기 전의 스코어보드는 다음과 같다.

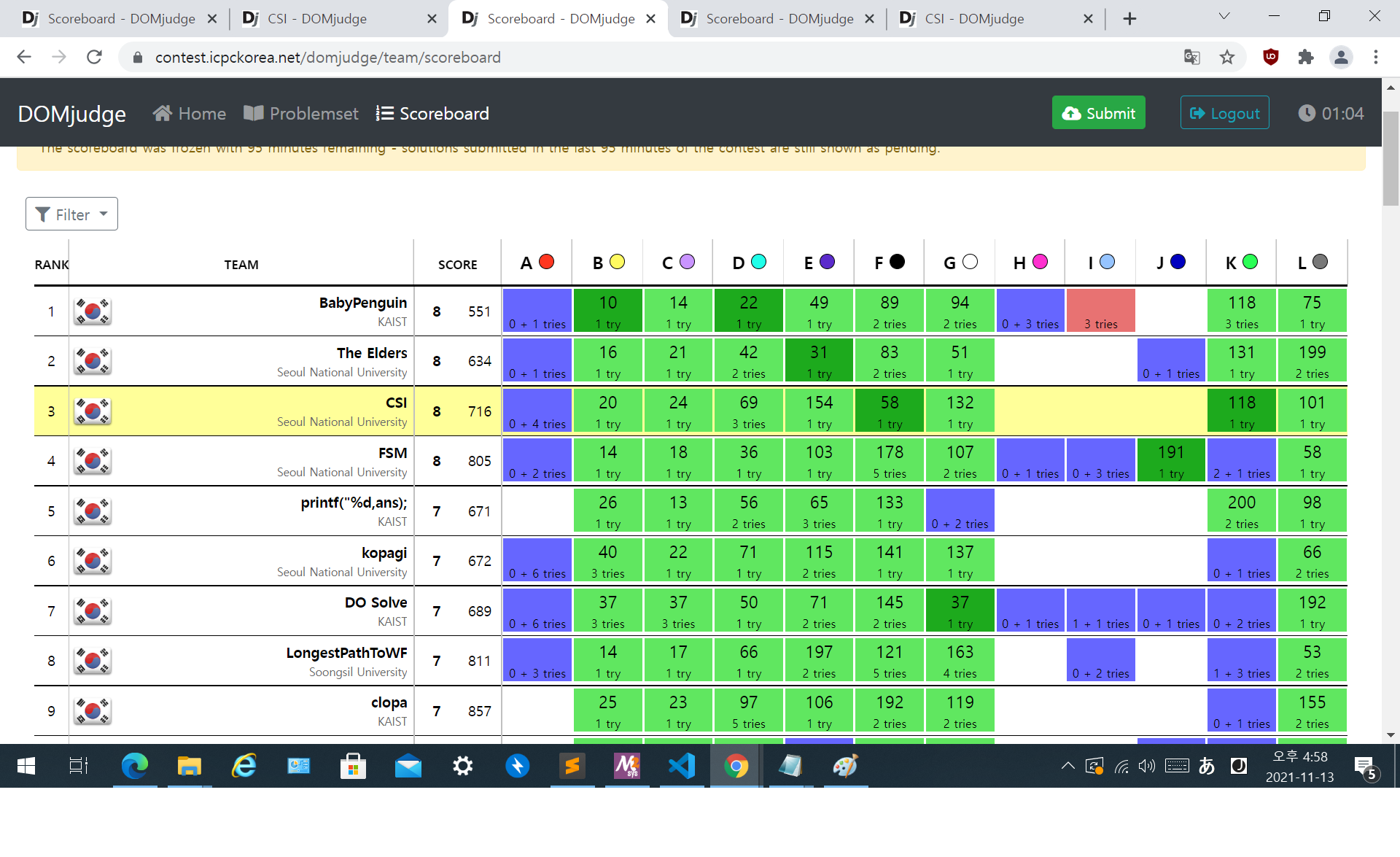
다른 팀들이 얼마나 풀었는지 모르겠지만, 꽤 높은 순위일 것이라 예상한 상태로 뒷정리를 마치고, 가까운 고깃집으로 갔다.

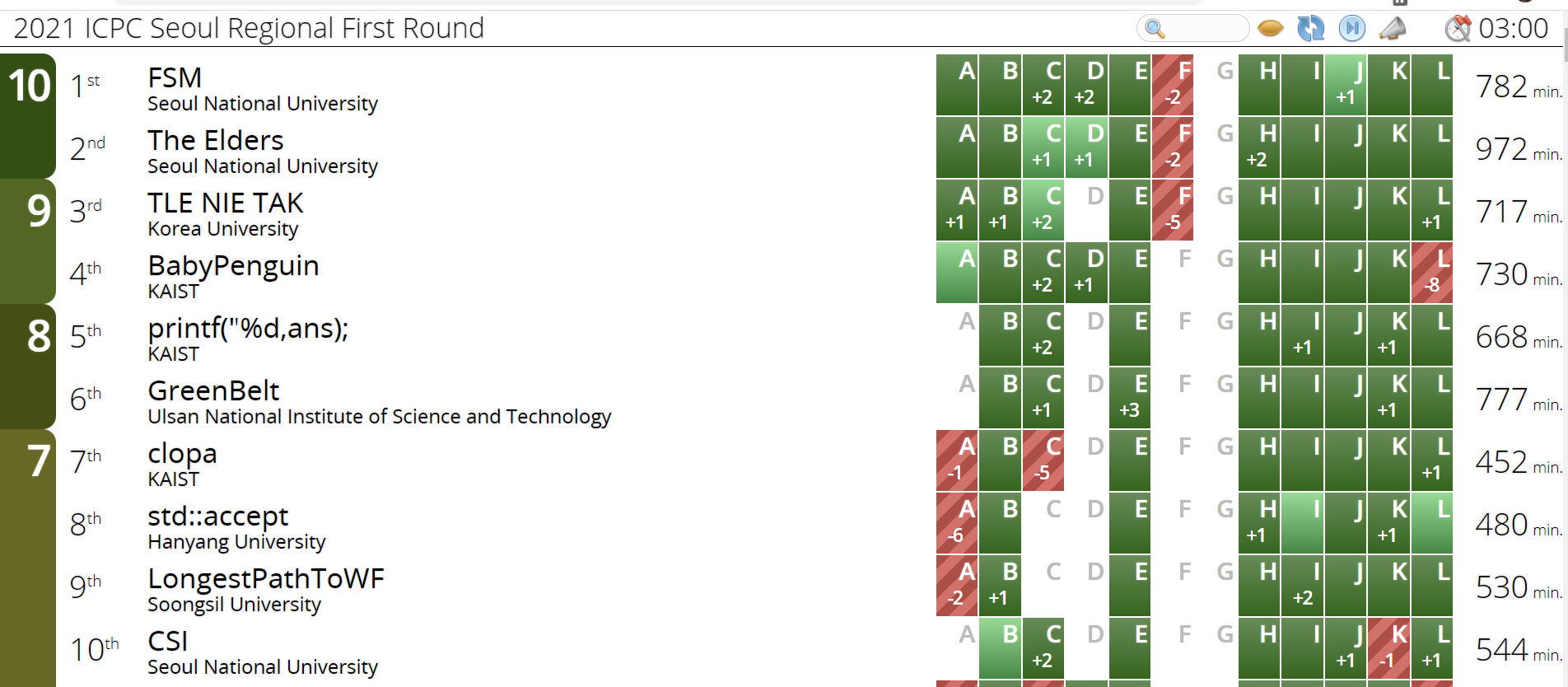
고깃집에서 식사를 하면서, 대회 결과 방송을 봤다. 프리즈가 풀리고 나서, 우리 순위는 다음과 같았다.

총평

전체 5등. 은상으로 대회를 마무리하게 됐다. 충분히 만족스런 성적이었다. 말이 씨가 된다고, 대회 전에 얘기했던 그 등수가 그대로 실제 등수가 됐다. J를 풀었더라면이라는 감정이 없다면 거짓말이지만, 우리 팀은 우리 팀이 할 수 있는 최선을 다했다고 생각한다.

본대회에서 난 우리 팀이 제출한 AC외의 제출을 혼자서 제출하며(…), 민폐가 될 뻔했지만, 다행히 A를 풀어서 어느 정도 상쇄를 할 수 있게 됐다.

대회 문제 풀이의 경우에는 내가 너무 늦게 글을 써서(..) 기억이 잘 나지 않고, 나중에 기회가 된다면 업소링을 하면서 업데이트를 하던가 할 예정이다. 그 외에 구사과님의 글에 풀이가 잘 나와 있다.

대회 본 시점과 이 글을 쓰는 시점이 약 6개월(..)간 차이가 있다. 너무 늦은 감이 있지만, 나와 함께 ICPC를 치른 CSI팀원 모두, 친절하게 ICPC 등록을 도와준 눕장 yclock, 마지막으로 매일 다이아 정도의 어려운 문제를 푸는 것을 요구하면서 실력을 향상시키는데 도움을 준 분들 모두에게 이 글을 통해 감사를 전한다.

더 읽어보기 »

작성일 | In |

들어가기 전에

ICPC 예선은 UCPC와 완전히 동일한 팀원으로 진행했다. 이미 UCPC 예선 후기글에서 간단히 언급했지만, 다시 한번 정리하자면

cs71107(CF,BOJ, 블로그 주인장) sait2000(CF,BOJ) IHHI(CF,BOJ)

이렇게 세 명으로 구성 돼있다.

팀명은 눈치 챌 사람은 눈치 챘겠지만, 각 멤버 핸들의 첫 글자를 따서 CSI 로 결정했다. 팀명은 내가 정했는데, 이렇다할 아이디어가 없어서 그냥 첫 글자 딴 CSI로 하자! 고 하니까 멤버들이 동의해서 결정됐다.

서울대의 경우, ICPC Regional 진출 여부를 문제 수로 컷하는 경우가 많았다. 만약 3~7위가 모두 동일한 수의 문제를 푸는 경우 (서울대의 경우 휴학생팀 제외 이번 대회에 총 12팀이 참가했다.) 3위도 자칫하면 떨어질 수 있다는 생각을 했다. 하지만 UCPC에서는 아주 좋은 결과를 내었기 때문에, UCPC 가 끝나고 나서 우리 팀 정도면 Regional에 갈 수 있지 않을까? 하는 생각을 하면서 준비했다.

대회 준비 과정

ICPC의 경우 UCPC와 달리 1컴으로 문제를 풀어야 하기 때문에, 지금까지와 달리 1컴으로 문제를 푸는 연습이 필요했다. 나의 경우 작년에 ICPC 참가 경험이 있기 때문에, 3컴, 1컴 차이가 얼마나 큰지 알고 있었고, 1컴으로 연습들을 진행하고자 했다.

ICPC 예선 연습을 총 3번 진행했는데, 첫번째, 두번째는 디스코드를 통해서 소통하며 3컴으로 진행했다. (디스코드를 통해 컴퓨터를 잡고 싶은 사람이 말하고, 특정시간대에는 한 사람만 키보드를 건드릴 수 있는 방식) 세번째는 직접 만나서 UCPC를 진행했던 slab이란 곳에서 진행했다.

첫번째 연습의 경우 2018 Jakarta Regional, 두 번째 연습은 GCPC 2018, 세 번째 연습은 NCPC 2019로 진행했다. 세번째 부터는 직접 만나서 진행했던 만큼, csi2021이라는 계정을 따로 파서 진행했다.

각 연습의 결과를 첨부한다.

2018 Jakarta Regional:

GCPC 2018:

NCPC 2019:

연습 결과를 보면 알겠지만, solved.ac 기준으로 다이아 이상의 문제를 밀지 못했다는 것을 알 수 있다. 하지만 플1을 포함한 플레 이하의 난이도는 확실히 밀어주는 모습을 보여주었기 때문에, 예선을 통과할 수 있을 거란 기대를 가졌다.

연습 때 프린트 문제가 이슈로 지적돼서 (원랜 동아리 방에서 출력이 가능했는데, 그날 이슈가 있어 프린트 문제 때문에 연습이 매우 지연되는 사태가 있었다.), 프린트가 가능한 스터디 카페를 물색하던 중, 서울대 입구 주변의 토즈 모임센터에서 진행하기로 결정했다. 프린트는 Sait님이 프린터기를 직접 가져오는(!) 것으로 해결.

대회 전날 Sait님과 함께 환경 점검 및 예비소집을 거치고 밥을 먹었다.

그 외에 팀노트의 경우 더불어민규당의 팀노트를 가져오고, 거기다가 센트로이드, 샤모스-호이 등 여러 가지 우리가 필요한 것들을 추가하고, 우리가 필요 없는 (general matching 가중치 있는 버전) 같은 것들을 제외시켰다.

팀노트에 있는 알고리즘들을 쓰는 문제들을 개인적으로 풀 수 있는 문제들을 그룹에 만들어두긴 했으나, 그다지 효과가 있었던 것 같지는 않다.

대회 진행 과정

14:00~ - 대회시작, 문제지가 통합돼있는 파일을 찾았으나 찾을 수가 없어서, 일단 급한 대로 각 문제들마다 뽑기로 하고 문제를 뽑기 시작했다. 이때 프린트 이슈 발생, 나중에서야 통합 파일이 올라온 것을 발견했다. 문제가 총 12문제였기에, 평소대로 ABCD가 나, EFGH는 Sait님, IJKL은 IHHI 가 맡아서 문제를 읽기 시작했다.

14:11 - IHHI가 I를 읽더니 이게 등록 문제 급이네요 ㅇㅇ 하더니 짜서 맞았다.

14:21 - 내가 A를 읽고 넘긴 후 B를 읽고 Sait신에게 넘기고 있을 때, IHHI가 J도 이렇게 하면 될 것 같다면서 열심히 짜고 제출했으나 결과는 WA, 디버깅 하더니 무슨 실수인지 알았다면서 고쳐서 바로 AC.

14:32 - B의 경우, 수학 스런 느낌이 나는 case work 문제였고, 처음엔 내가 풀 수 있을 줄 알고 덤볐으나 케이스가 있다는 걸 깨닫고 이런 걸 우리 팀에서 제일 잘하시는 Sait신에게 토스, Sait신에게 문제 설명과 약간의 대화를 거친 후, Sait신이 열심히 풀이 구체 및 구현을 마치고 AC. (B 퍼솔!)

이 시점에서 스코어보드 상 우리가 1위였다.

여기까지 온 이후, C의 경우 난 풀이가 잘 생각이 안 나서 일단 넘긴 상태였고, D를 잡아보려고 한 상태였다.

14:54 - 스코어보드를 보니, H, E가 풀린 상태여서 보니 H가 IDT나 segtree를 사용하면 쉽게 풀리는 문제여서, 내가 잡았다. IDT를 통해서 빠르게 구현하고 예제가 나오는 것을 확인후, 제출. AC.

15:20 - 내가 H를 열심히 풀 동안 Sait과 IHHI는 C를 잡고 고민하고 있었다. C의 풀이를 대략적으로 알아냈고, 내가 H를 푼 후 제출했으나 WA. 나와 IHHI가 디버깅에 들어갔고, Sait신은 E를 잡았다. C의 케이스 처리 두 개를 못해준 것을 제출 하나당 발견해서, 2틀 후 AC.

15:30 - Sait신이 E의 입력 크기를 통해 추론한 dp풀이가 정당하다고 판단해서 코딩했으나, 결과는 예제 컷이 나왔다. 공식 사용도 완벽했기 때문에, 뭐가 문제인지 알 수 없었는데, 내가 Sait신이 실수 나눗셈을 해야 하는데 정수 나눗셈을 한 것을 발견했다. (파이썬에 익숙하신 나머지 정수 나눗셈은 //, 그냥 나눗셈을 /로 생각해서 발견하기 힘들었던 것) 그리고 그 부분을 고친 후 예제가 통과하는 것을 발견. 제출 후 AC.

Sait신이 E를 해결할 동안, 나와 IHHI는 L을 고민했고, 크기상 이정도면 O(n^3)이 돌지 않을까? 라고 생각하면서 풀이를 찾아냈고, IHHI가 L을 구현하는 동안 나와 Sait신은 A를 고민했으나, 잘 풀리지 않고 있었다.

L에서 IHHI의 구현이 예제가 잘 나왔으나 AC를 받지 못했고, 당연히 WA일 것이라 생각한 우리는 신나게 디버깅을 하고 있었다. 하지만 도저히 WA 원인을 찾을 수가 없었고, 그때 Sait신은 자신의 A 풀이를 구현하고 있었으나 맞을 거라는 확신이 없는 상태였다. 풀린 문제 중 우리가 못 푼 문제가 A,K,L 정도였기 때문에, L의 디버깅을 잠시 쉬고 K를 봤으나 역시 유의미한 성과는 없었다.

15:43 - K 풀이를 나와 Sait신이 열심히 토론하던 중에, IHHI가 이렇게 하면 안 되냐고 해서 K를 구현하고 제출했으나, (대충 세그트리를 쓰는 풀이였던 걸로 기억한다.) WA를 받았다. 이대로 6솔로 끝나는 건가? 싶던 중…

IHHI가 제출 내역을 보더니 K결과가 WA가 아니라 TLE(….) 라는 소식을 전했다. 대회 종료 17분이 남은 시점에서, 우리는 급히 L 풀이의 복잡도를 끌어내리는 작업에 들어갔다. Sait신과 IHHI가 동시에 달라붙어서 코딩에 들어갔고, 나는 A,K 를 다시 한번 보고 있었다.

15:55 - 제출한 코드가 예제컷 나는 광경을 지켜보면서 가슴이 철렁하는 경험을 몇 번 하고, (상황이 급박해서 난 예전 코드에 pragma gcc를 박은 코드라도 제출해보자는 의견도 냈었다.) 드디어 예제가 나오는 코드가 완성 됐다. 그리고 떨리는 마음으로 제출… 그리고 그 코드는 AC를 받았다! 그렇게 우리는 종료 5분전에(…) 7솔을 달성할 수 있었다.

대회 결과

대회가 끝나고 나서 전체 순위는 그리 나쁘지 않을 것으로 예상됐지만, 서울대 내 순위가 중요했기 때문에 수소문한 결과, 내가 얘기했던 대로 서울대 내 3~7위 팀이 전부 7솔이라는 사실을 알아챘다.

그전까지 서울대는 문제 수로 컷을 냈기에 최악의 경우 이번에도 예선 탈락을 경험할 수 있을 것이란 불안감을 가지고 밥을 먹으러 갔다.

스코어보드가 나오자 서울대 내 3위라는 것을 알게 됐고, 웬만하면 진출할 것이라고 생각했다.

그 후 본선팀 발표에서 문제 수 컷이 6솔로 확정됐고, 서울대는 우리 팀을 포함해 총 7팀이 진출이 확정됐다.

당시 스코어보드

전체 스코어보드는 여기에서 확인 가능하다.

총평

여러 모로 아쉬움이 많이 남는 대회였다. 우선, TLE를 WA로 착각하여 의미없는 데에 상당한 시간을 낭비했다. 또한, 연습 때와 마찬가지로 여전히 solved.ac 기준 다이아 급의 문제를 밀지 못했다.

K의 경우 난이도를 볼 때 우리 팀 정도면 충분히 밀 수 있었던 문제로 보이나, L에 집중해야 했고 & 거기다가 약간 발상 단계에서 말리는 바람에 풀지 못했다.

A의 경우 그냥 아이디어를 떠올릴 시간이 부족했던 것으로 보인다.

프린트 이슈부터 시작해서 여러모로 아쉬운 점이 많은 대회였다.

문제 풀이

UCPC 후기 처럼 내가 풀이를 갖고 있는 문제들에 한해서 서술한다. 업솔빙을 진행함에 따라 여기에 풀이가 추가될 수 있음.

전체 문제에 대한 풀이는 구사과님의 블로그 글에 나와있으니 참고하기 바란다.

A. Best student

대회 중엔 풀지 못했던 문제,

구간이 여러 개 주어지고, 해당 구간내에 가장 자주 등장한 값 중에서, 가장 큰 값을 출력해야 한다.

아마 이 글을 읽는 사람들이라면 아마 대부분 수열과 쿼리문제들을 떠올릴 것이다.

일단 업데이트가 없고, 뭔가 세그 트리로 처리하긴 어려워 보이니 Mo’s Algorithm을 써야 하긴 할 것 같아 보인다.

하지만 그냥 구간에 대해서 bucket을 나누어선 풀기 어렵다. 나도 들은 풀이지만, 내가 접근한 방법은

바로 수들에 대해서도 구간을 나누는 것이다. 현재 배열 내에 서로 다른 수가 많아봤자 $N$개가 있으니, $\sqrt(N)$개로 버킷을 나눈 후, 각각의 버킷에 대해 속하는 수들에 대해 가장 자주 등장하는 수가 현재 몇 번 등장하는지를 관리해준다.

그렇게 업데이트를 진행하면, 큰 수들이 속하는 버킷부터 훑으면서 전체에서 정답이 속하는 버킷이 어디인지 찾고 (이 과정에서 $O(\sqrt(N))$)가 걸린다. 그리고 그 버킷 내에서 다시 정답을 찾는다. (다시 $O(\sqrt(N))$)이 걸린다.) 이렇게 하면 총 시간 복잡도

$O((N+Q)\sqrt(N))$에 풀수가 있다. 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
pii query[MAXN];
vector<pii> qq[330];

int cal[2*MAXN];
int vv[330];
int ccal[330][MAXN];

int ans[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1,idy = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>q;

    vector<int> pos;

    for(int i=0;i<n;i++){
        cin>>A[i];
        pos.push_back(A[i]);
    }

    const int sqn = (int)sqrt(n);

    for(int i=0;i<q;i++){
        cin>>a>>b;
        query[i] = pii(a-1,b-1);
        qq[(a-1)/sqn].push_back(pii(b-1,i));
    }

    sort(pos.begin(),pos.end());
    pos.erase(unique(pos.begin(),pos.end()),pos.end());

    m = (int)pos.size();

    const int sq = (int)sqrt(m);

    for(int i=0;i<n;i++){
        A[i] = lower_bound(pos.begin(),pos.end(),A[i])-pos.begin();
    }

    const int esq = (n-1)/sqn;

    for(int i=0;i<=esq;i++){
        sort(qq[i].begin(),qq[i].end());
    }

    const int msq = (m-1)/sq;

    for(int i=0;i<=msq;i++){
        ccal[i][0] = sq;
    }

    cur = A[0];

    a = cur/sq;

    cal[cur] = 1;

    ccal[a][0]--;
    ccal[a][1]++;

    vv[a] = 1;

    int st = 0,en = 0;

    for(int i=0;i<=esq;i++){

        const int cursz = (int)qq[i].size();

        for(int j=0;j<cursz;j++){

            idx = qq[i][j].s;

            x = query[idx].f;
            y = query[idx].s;

            for(int t=st-1;t>=x;t--){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]++;

                ccal[a][cnt]--;
                ccal[a][cnt+1]++;

                if(!(vv[a]^cnt)){
                    vv[a]++;
                }
            }

            for(int t=en+1;t<=y;t++){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]++;

                ccal[a][cnt]--;
                ccal[a][cnt+1]++;

                if(!(vv[a]^cnt)){
                    vv[a]++;
                }
            }

            for(int t=st;t<x;t++){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]--;

                ccal[a][cnt]--;
                ccal[a][cnt-1]++;

                if((!ccal[a][cnt])&&(!(cnt^vv[a]))){
                    vv[a]--;
                }
            }

            for(int t=en;t>y;t--){
                cur = A[t];

                a = cur/sq;
                cnt = cal[cur];

                cal[cur]--;

                ccal[a][cnt]--;
                ccal[a][cnt-1]++;

                if((!ccal[a][cnt])&&(!(cnt^vv[a]))){
                    vv[a]--;
                }
            }

            st = x;
            en = y;

            mx = 0;
            idy = -1;

            for(int t=msq;t>=0;t--){
                if(mx<vv[t]){
                    mx = vv[t];
                    idy = t;
                }
            }

            assert(mx>0);

            cur = idy*sq;

            for(int t=cur+sq-1;t>=cur;t--){
                if(cal[t]^mx)continue;
                ans[idx] = t;
                break;
            }
        }
    }


    for(int i=0;i<q;i++){
        cur = ans[i];
        cout<<pos[cur]<<"\n";
    }


    return 0;
}

H. Similarity

결국 두 수열 $p, q$에 대해서, $p_{i} < p_{j} < p_{k} $이고 $q_{i} < q{j} < q_{k}$인 $i,j,k의 개수를 세라는 것이므로,

저 위의 조건에서 $j$ 기준으로 생각하면, 결국 답은

각각의 $j$에 대해서, 가능한 $i$의 개수와 $k$의 개수를 곱한 것을 전부 더한 값이다.

그리고 $j$에 대한 $i$의 개수는 $p_{i} < p_{j}$이고 $q_{i} < q_{j}$인 개수를 세는 것인데, 이는 널리 알려져 있다 시피 segment tree등을 활용하면 쉽게 셀 수 있다.

비슷하게 $j$에 대한 $k$의 개수도 셀 수 있다.

코드는 다음과 같다. 복잡도는 $O(NlogN)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>
#define f first
#define s second
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
const int MAXN = 2e5+10;
const int MAXNN = 1e6+10;
pii A[MAXN];

vector<int> pp[MAXNN];
int tree[MAXNN*4];

int Lv[MAXN];
int Rv[MAXN];

inline void update(int tmp){

    while(tmp){
        tree[tmp]++;
        tmp>>=1;
    }
    return;
}

inline int getans(int L,int R){
    int res = 0;
    while(L<=R){
        if(L&1){
            res += tree[L];
            L++;
        }
        if(!(R&1)){
            res += tree[R];
            R--;
        }
        L>>=1; R>>=1;
    }
    return res;
}

int main(){

    int n;
    int mx = 0;
    int my = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(0);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>A[i].f;
        mx = max(mx,A[i].f);
    }

    for(int i=1;i<=n;i++){
        cin>>A[i].s;
        my = max(my,A[i].s);
    }

    for(int i=1;i<=n;i++){
        pp[A[i].f].push_back(i);
    }

    int base = 1;

    for(;base<=my;base<<=1);

    int cursz = 0;
    int idx = 0;

    for(int i=0;i<=mx;i++){
        cursz = (int)pp[i].size();

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            Lv[idx] = getans(base,base+A[idx].s-1);
        }

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            update(base+A[idx].s);
        }
    }

    fill(tree,tree+MAXNN*4,0);

    for(int i=mx;i>=0;i--){
        cursz = (int)pp[i].size();

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            Rv[idx] = getans(base+A[idx].s+1,base+my);
        }

        for(int j=0;j<cursz;j++){
            idx = pp[i][j];
            update(base+A[idx].s);
        }
    }

    ll res = 0;

    for(int i=1;i<=n;i++){
        res += (1LL*Lv[i]*Rv[i]);
    }

    cout<<res<<"\n";

    return 0;
}

I. Sport Climbing Combined

그냥 정렬 기준을 세워서 함수를 짠 다음 정렬 시켜주면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

struct P{
    int va,vb,vc;
};

bool cmp(const P&p,const P&q){
    if(!(p.va^q.va)){
        if(!(p.vb^q.vb))return p.vc<q.vc;
        else return p.vb<q.vb;
    }
    else {
        return p.va<q.va;
    }
}

P A[110];

int main()
{
    int n,m,k,a,b,c,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>k>>a>>b>>c;
        A[i] = {a*b*c,a+b+c,k};
    }

    sort(A+1,A+n+1,cmp);

    for(int i=1;i<=3;i++){
        cout<<A[i].vc<<" ";
    }
    cout<<"\n";

    return 0;
}

J. Ten

여러 가지 방법이 있겠으나, 현재 제한 조건 상 각 셀의 수는 반드시 양의 정수이고, 정확히 10인 것만 세면 되므로, 후보로 가능한 직사각형의 넓이는 10을 넘을 수 없다.

따라서 오른쪽 아래 점 후보로 가능한 모든 점을 순회하면서 후보 직사각형 (넓이가 10이하)인 것들을 모두 확인하는 것으로도 충분히 시간안에 돌아간다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[510][510];
int psum[510][510];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>A[i][j];
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            psum[i][j] = A[i][j]+psum[i-1][j]+psum[i][j-1]-psum[i-1][j-1];
        }
    }

    int res = 0;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){

            for(int t=1;t<=10;t++){

                if(i<t)break;

                idx = min(10/t,j);

                for(int tt=1;tt<=idx;tt++){
                    cur = psum[i][j]-psum[i-t][j]-psum[i][j-tt]+psum[i-t][j-tt];
                    if(cur==10)res++;
                }
            }
        }
    }

    cout<<res<<"\n";

    return 0;
}

K. Treasure Hunter

대회 중에 못 풀었던 문제로, 우리 팀의 수준이라면 풀 수 있었을 텐데 하고 아쉬움이 남는 문제이다. 아마 대회 당시엔 말렸던 것 같다.

문제에서 원하는 것은 결국 (증명은 아직 잘 모르겠지만) LIS로 환원시킬 수 있고, 좌표를 적절하게 변환한 후 LIS를 구해주면 된다.

복잡도는 $O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

vector<int> id[MAXN];

int val[MAXN];
int tree[MAXN*4];

int getans(int L,int R)
{
    int res = 0;
    while(L<=R){
        if(L&1){
            res = max(res,tree[L]);
            L++;
        }
        if(!(R&1)){
            res = max(res,tree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }
    return res;
}

void update(int tmp,int v)
{
    while(tmp){
        tree[tmp] = max(tree[tmp],v);
        tmp>>=1;
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m>>k;

    for(int i=1;i<=k;i++){
        cin>>y>>x;
        y = n-y;
        id[x].push_back(y);
    }

    int base = 1;
    for(;base<n;base<<=1);

    for(int i=1;i<=m;i++){

        for(int j=0;j<(int)id[i].size();j++){
            idx = id[i][j];
            cur = getans(base,base+idx-1)+1;

            val[j] = cur;
        }

        for(int j=0;j<(int)id[i].size();j++){
            idx = id[i][j];
            update(base+idx,val[j]);
        }
    }

    cout<<tree[1]<<"\n";


    return 0;
}
더 읽어보기 »

작성일 | In |

들어가기 전에

UCPC 본선은 올해 8월 14일에 있었고, 이 글을 쓰는 지금이 11월 17일이니까, 무려 3달이 넘었다. 그동안 본선 후기를 못 쓴 핑계를 대자면, 대회가 끝나고 얼마 지나지 않아서 랩 인턴 지원이라던가, 정보처리산업기사 시험 접수라던가 하는 일들이 있었고, 학기 때는 학기와 ICPC에 이리 치이고 저리 치여서 후기를 쓰지 못했다.

이제 ICPC도 끝났고, 학기 관련해서도 중간고사가 끝나고 과제도 당장 급한 게 없어서, 늦었지만 후기를 써보려 한다.

최대한 정확하게 쓰려 하지만, 시간이 오래 지났기 때문에 부정확할 수 있다. 양해 바란다.

대회 준비 과정

앞선 UCPC 예선의 결과가 굉장히 좋은 편이었기 때문에 (4위), 본선에도 높은 순위를 기대할 수 있지 않을까? 하는 기대가 있었다.

예선과 본선 간에 약 2주의 시간이 있었고, 방학이었으나, 각자 일정 때문에 연습을 그리 많이 잡지는 못했다.

UCPC는 3컴이었기 때문에 모이지 않고, 디스코드와 각자 컴을 사용해서 연습 했다.

본선 연습으로는 2017 Tsukuba regional과, GCPC 2019를 돌았다.

이때 팀연습 결과를 첨부한다.

2017 Tsukuba:

GCPC 2019:

위의 결과에서 볼 수 있다시피 2017 Tsukuba의 경우 solved.ac 기준 다이아 2 이상 문제를 제외한 모든 문제를 풀었고, GCPC 2019의 경우 올솔브를 했다.

그래서 UCPC 본선도 기대하며 준비할 수 있었다. 다만, 위의 결과에서 보다시피 내 기여가 좀 적었기 때문에… 난 본선에선 좀 더 기여를 하자고 다짐하면서 준비했다.

대회 진행 과정

대회 장소는 서울대의 윗공대 301동의 slab이란 곳으로 정했다. 시간은 대회 당시 시간 (KST 기준)이다.

11:00 - 대회시작, 평소대로 내가 A,B,C,D를 Sait신이 E,F,G,H를 , 그리고 IHHI가 I,J,K,L을 잡았다.

11:00 ~ 11:20 - 대회시작 부터 이때까지, 문제들이 전체적으로 쉽지 않다는 것을 깨달았다. A의 경우 대략적인 풀이를 알아냈지만, 그것을 구체화 시키고 구현하는 것보단 그냥 넘어가는게 맞다는 판단을 내렸다 그리고 B,C를 읽었지만 풀이에 접근조차 하지 못했다. 대충 분위기를 확인해보니까 다른 팀원들도 비슷한 분위기 같았다. (나중에 solve.ac 기준 난이도를 보니 Sait님의 H가 유일한 골드였고, IHHI는 잡았던 문제 중 가장 쉬운 문제가 플1 이었다.)

11:20 - D를 읽고 나서 빠르게 구현하면 되는 문제라는 것을 알아냈고, 구현했다. 바로 AC. 이때부터 난 A를 구현하기 시작했다.

11:29 - Sait님이 H가 적당히 풀만한 문제이나, 본인은 빠르게 구현할 자신이 없다고 하시며 IHHI에게 토스. IHHI가 구현해서 AC.

12:03 - D 이후 A를 내가 꾸준히 구현하고 있었고, 구현을 끝낸 후 제출 한번만에 AC를 받았다.

12:29 - 내가 A관련해서 씨름할 때 Sait신이 K를 읽은 후 이거 킹전 지식 문젠데?를 시전하셨고, 나도 처음들어보는 사전 지식을 언급하며 이걸 알면 케이스 워크라고 하시면서 슥슥 구현하고 계셨고, IHHI는 J를 잡고 구현하고 있었다. 그리고 IHHI는 J를 제출했찌만 아쉽게 WA가 떴고, 거의 바로 Sait신이 K를 퍼솔했다.

12:36 - IHHI가 J를 고쳐서 맞았다. 5솔.

12:36 ~ 13:18 - 이제 대충 풀만한 문제가 어떤 문제들인지 대충 나온 상태였기 때문에, Sait,IHHI가 E를 고민하고, 난 F를 잡았다. F를 보니 Taxi 거리의 성질을 이용하면 되는 문제라고 판단했다. 단, 내 풀이는 구현이 좀 걸렸다. 하지만 그때 당시 이 풀이를 빠르게 이해하고 구현할 수 있는 사람이 나라서, 그냥 내가 구현하기로 했다.

13:18 - 짜고 난 코드를 돌려보니 예제컷이 나서 멘붕을 경험한 후 코드를 좀 고치니 바로 예제가 나왔고, 그냥 제출했다. AC.

13:18~13:54 - 스코어 보드 상에선 E가 많이 풀려있었기 때문에, E를 빠르게 밀어야 한다는 판단을 했다. 나와 IHHI, Sait이 모두 고민했다. 그러던 중 IHHI가 그냥 이렇게 가면 되는 것 아니냐?라고 한 후 구현을 시작했다.

13:54 - E 구현을 마친 후 AC.

13:54 ~ 종료 시까지 - 대충 스코어보드를 봤을 때, B,L은 사람이 풀게 아니다!라는 결론을 내렸고, Sait님은 자기분야?인 G를 계속 고민했으나 이거다 하는 풀이를 찾지 못하고 있었다. 결국 도전할 만한 건 C,I 였고, 구현 문제 같은 C를 IHHI, Sait이 맡고, I를 내가 가져가기로 하고 각자 고민과 구현을 시작했다. 그러나 종료 5분전 제출한 내 구현은 여지 없이 WA가 나왔고, IHHI,Sait이 각자 C를 구현했으나 제한 시간 내에 구현하지 못했다. 그리고 그대로 대회가 끝났다.

대회 결과

비록 C,I를 못 풀긴 했으나, 높은 순위일 것으로 예측하고 있었고, 우린 정리를 한 후 윗공대 명물(?)인 300동 식당에서 저녁을 먹었다. 저녁을 먹으면서 못 푼 문제들 풀이를 들으니 C는 구현이 맞았고, I는 놀랍게도(?) 플로우여서 좀 허탈했다.

그리고 스코어보드 까는 방송을 시청했다.

그리고 결과는 다음과 같이 5위(!!!)라는 매우 높은 수상을 받을 수 있었다.

7솔브 팀이 꽤 많았는데, 우리 팀 패널티 관리가 나쁘지 않았던 것 같다.

대회 총평

UCPC 2021 도 solved.ac 기준 골드 1 - 플레 5 - 다이아 3 - 루비 1이라는 어려운 셋이었다.

하지만 초반에 말리지 않고 각자 역할 분배를 확실하게 해서 패널티를 줄이고, 무엇보다 Sait신이 K를 퍼솔해준 게 수상에 큰 역할을 했다.

그리고 이번 셋에선 내가 혼자서 3개를 밀었기 때문에 유의미한 기여를 했고, IHHI 역시 3개를 풀었다. 그리고 Sait신은 비록 K하나를 풀었지만, 수상 결정에 있어서 가장 중요했던 K를 풀어주는 역할을 수행했다.

각자가 잘하는 것들을 잘 분배해서 해결한 것이 높은 순위를 가져온 동력이 됐다고 생각한다.

5등상 상품은 데브시스터즈에서 지원해줬다. 에어팟 잘 쓰겠습니다~

문제 풀이

출제된 문제들 중 내가 백준에서 푼 것들에 대해서 풀이를 작성한다.

다른 문제들의 경우 내가 업솔빙을 진행함에 따라 여기에 업데이트 할 것 같다.

문제들은 여기에서 확인가능하다.

A. A+B와 쿼리

문제를 요약하면, A,B 두 10진수 정수가 있고(크기가 아주 크다.) A,B의 특정 자리수를 바꾸는 쿼리가 주어진다.

그리고 쿼리가 주어질 때마다, C = A+B를 계산한 후, 쿼리가 주어지기 이전과 비교해서 ‘달라진 자릿수의 개수’가 몇개인지 묻는 문제이다.

우선 우리가 신경 써야 할 것이 받아올림이란 것은 쉽게 생각할 수 있다.

편의상 A,B를 각 원소가 0~9인 길이 N 짜리 정수 배열로 보자. 그리고 $i$ 번째 자리수를 $A[i],B[i]$라고 두자.

그리고 문제의 조건상, 각 자릿수에 대해서 생각하면 그 전에 올라오는 자릿수의 받아 올림 값은 0,1 중에 하나다.

그럼 각 자릿수에 해당하는 수들의 합에 따라 케이스를 나눠 보자.

$A[i]+B[i] \geq 10$인 경우 : 올라오는 자릿수의 받아 올림 값에 상관 없이 1을 올린다.

$A[i]+B[i] = 9$인 경우 : 올라오는 자릿수의 받아 올림 값에 따라 넘기는 값이 바뀐다.

$A[i]+B[i] \leq 8$인 경우 : 올라오는 자릿수의 받아 올림 값에 상관 없이 0을 올린다.

이렇게 경우를 나눠서 생각하면 받아 올림이 계속 올라가다가 첫번째, 세번째 케이스에 해당하는 경우를 처음 만났을 때, 이전 결과에 대해 자릿수가 바뀌는 경우가 끝난다는 것을 알 수 있다.

즉 우리가 해줘야 하는 것은

  • 각 $i$에 대해 $A[i]+B[i]$가 위의 3가지 경우 중 어디에 속하는지 관리
  • 그 관리하는 정보를 바탕으로 문제에서 원하는 정답을 구하기

로 나눌 수 있다.

현재 쿼리에 의해 업데이트가 일어나고, 전체 배열에 대해 답을 빠르게 구해야 하므로, 세그 트리(또는 인덱스 트리)를 통해서 관리해줘야 겠다는 생각을 할 수가 있고 실제로 가능하다.

업데이트가 들어올 때마다 결과가 어떻게 바뀌는지 계산하고, 현재 자리수에 해당하는 경우가 1,3번째인지, 2번째인지에 따라 업데이트한다.

계산의 경우 현재 업데이트에 의해서 1,3번째경우에서 2번째 경우로 바뀌는지 또는 그 반대인지 여부를 검사하고, 그에 따라 답을 계산한다.

자세한 계산은 코드를 참고하라. 구간의 min을 계산하는 IDT와 max를 계산하는 IDT를 사용하고 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 3e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int B[MAXN];
char S[MAXN];
char T[MAXN];

int tree[MAXN*4];
int ttree[MAXN*4];

inline void update(int tmp,int v,int vv){

    tree[tmp] = v;
    ttree[tmp] = vv;

    tmp>>=1;

    while(tmp){
        tree[tmp] = max(tree[(tmp<<1)],tree[(tmp<<1)|1]);
        ttree[tmp] = min(ttree[(tmp<<1)],ttree[(tmp<<1)|1]);
        tmp>>=1;
    }

    return;
}

inline int getmx(int L,int R){

    int res = -INF;

    while(L<=R){
        if(L&1){
            res = max(res,tree[L]);
            L++;
        }
        if(!(R&1)){
            res = max(res,tree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}


inline int getmn(int L,int R){

    int res = INF;

    while(L<=R){

        if(L&1){
            res = min(res,ttree[L]);
            L++;
        }
        if(!(R&1)){
            res = min(res,ttree[R]);
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}

inline int isup(int idx,int base){

    if(A[idx]+B[idx]<9)return 0;

    if(A[idx]+B[idx]>9)return 1;


    int ii = getmn(base+idx+1,(base<<1)-1);

    if(ii==INF)return 0;
    else if(A[ii]+B[ii]<9)return 0;
    else return 1;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    char ty;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>q;

    cin>>S+1;
    cin>>T+1;

    int base = 1;

    for(;base<=n;base<<=1);

    tree[base] = 0;
    ttree[base] = 0;

    for(int i=1;i<=n;i++){
        A[i] = S[i]-'0';
        B[i] = T[i]-'0';

        if(A[i]+B[i]==9){
            tree[base+i] = -INF;
            ttree[base+i] = INF;
        }
        else {
            tree[base+i] = i;
            ttree[base+i] = i;
        }
    }

    for(int i=n+1;i<base;i++){
        tree[base+i] = -INF;
        ttree[base+i] = INF;
    }

    for(int i=base-1;i>=1;i--){
        tree[i] = max(tree[(i<<1)],tree[(i<<1)|1]);
        ttree[i] = min(ttree[(i<<1)],ttree[(i<<1)|1]);
    }

    int v;

    int preup = 0;
    int curup = 0;

    int res = 0;
    int curidx = -1;

    for(int i=0;i<q;i++){
        cin>>ty>>idx>>v;

        idx = (n-idx+1);

        if(ty=='A'){
            if(A[idx]==v){
                cout<<0<<"\n";
            }
            else {

                preup = isup(idx,base);

                A[idx] = v;

                curup = isup(idx,base);

                if(preup^curup){
                    curidx = getmx(base,base+idx-1);
                }
                else {
                    curidx = idx;
                }

                cout<<(idx-curidx+1)<<"\n";

                if((A[idx]+B[idx])==9)update(base+idx,-INF,INF);
                else update(base+idx,idx,idx);
            }
        }
        else {
            if(B[idx]==v){
                cout<<0<<"\n";
            }
            else {

                preup = isup(idx,base);

                B[idx] = v;

                curup = isup(idx,base);

                if(preup^curup){
                    curidx = getmx(base,base+idx-1);
                }
                else {
                    curidx = idx;
                }

                cout<<(idx-curidx+1)<<"\n";

                if((A[idx]+B[idx])==9)update(base+idx,-INF,INF);
                else update(base+idx,idx,idx);
            }
        }
    }


    return 0;
}

D. 츠바메가에시

문제 설명은 생략한다.

결국 경우의 수가

  • x 축에 평행한 3개
  • x 축에 평행한 것 2개에 y 축에 평행한 것 1개
  • x 축에 평행한 것 1개에 x 축에 평행한 것 2개
  • y 축에 평행한 것 3개

이 4가지 경우 밖에 없음을 알 수 있다.

이 4가지 각각에 대해서 전부 해당 경우의 답을 계산하면 되는데,

앞의 두 개를 계산 가능하면 뒤에 두 개도 비슷하게 계산 가능하므로 앞의 두 개만 설명한다.

x 축에 평행한 3개의 경우 각 y 좌표에 대해 값들의 합을 저장하는 배열을 만들고 입력을 순회하면서 계산 해준뒤, 중복이 생기지 않게 주의하면서 가장 합이 큰 3개의 합을 구하면 된다.

x 축에 평행한 것 2개에 y 축에 평행한 것 1개의 경우 우선 y 축에 평행한 것 1개를 기준으로 생각한다.

각 x 좌표를 순회하면서, y축에 평행한 참격의 좌표를 현재 좌표로 했을 때, x 축에 평행한 참격 2개를 한다고 할 때의 얻는 최댓값을 계산하면 된다. 겹치는 제비의 경우, 한번만 세지므로, 해당 x 좌표의 제비들을 계산하기 전에 미리 제거 한 후, 그때의 답을 계산하고, 다음 좌표로 넘어갈 때 다시 복원시켜준다고 생각하면 풀이의 방향을 잡기 쉽다.

따라서 이 문제도 업데이트와 계산이 필요한 문제로 바꿀 수 있고, 이는 세그 트리 및 오프라인 쿼리를 사용해서 계산 가능하다.

코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e6+10;
const int MAXM = 1e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int yv[MAXN];
int xv[MAXN];

vector<pii> xval[MAXN];
vector<pii> yval[MAXN];

pii tree[MAXN*4];

inline void update(int tmp,int v){

    tree[tmp].f+=v;
    tmp>>=1;

    while(tmp){

        if(tree[(tmp<<1)].f>tree[(tmp<<1)|1].f){
            tree[tmp].f = tree[(tmp<<1)].f;
            tree[tmp].s = max(tree[(tmp<<1)].s,tree[(tmp<<1)|1].f);
        }
        else {
            tree[tmp].f = tree[(tmp<<1)|1].f;
            tree[tmp].s = max(tree[(tmp<<1)|1].s,tree[(tmp<<1)].f);
        }

        tmp>>=1;
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    int xmx = 0;
    int ymx = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++)
    {
        cin>>x>>y>>a;
        xval[x].push_back(pii(y,a));
        yval[y].push_back(pii(x,a));
        xv[x]+=a;
        yv[y]+=a;
        xmx = max(xmx,x);
        ymx = max(ymx,y);
    }

    int res = 0;

    int mx1 = 0,mx2 = 0;

    for(int i=0;i<=xmx;i++){
        cur = xv[i];
        if(mx<cur){
            mx2 = mx1;
            mx1 = mx;
            mx = cur;
        }
        else if(mx1<cur){
            mx2 = mx1;
            mx1 = cur;
        }
        else {
            mx2 = max(mx2,cur);
        }
    }

    res = max(res,(mx+mx1+mx2));

    mx = 0;
    mx1 = 0;
    mx2 = 0;

    for(int i=0;i<=ymx;i++){
        cur = yv[i];
        if(mx<cur){
            mx2 = mx1;
            mx1 = mx;
            mx = cur;
        }
        else if(mx1<cur){
            mx2 = mx1;
            mx1 = cur;
        }
        else {
            mx2 = max(mx2,cur);
        }
    }

    res = max(res,(mx+mx1+mx2));

    int base = 1;

    for(;base<=ymx;base<<=1);

    for(int i=0;i<=ymx;i++){
        tree[i+base] = pii(yv[i],0);
    }

    for(int i=ymx+1;i<base;i++){
        tree[i+base] = pii(0,0);
    }

    for(int i=base-1;i>=1;i--){
        if(tree[(i<<1)].f>tree[(i<<1)|1].f){
            tree[i].f = tree[(i<<1)].f;
            tree[i].s = max(tree[(i<<1)].s,tree[(i<<1)|1].f);
        }
        else {
            tree[i].f = tree[(i<<1)|1].f;
            tree[i].s = max(tree[(i<<1)|1].s,tree[(i<<1)].f);
        }
    }

    for(int i=0;i<=xmx;i++){
        for(int j=0;j<(int)xval[i].size();j++){
            idx = xval[i][j].f;
            cur = xval[i][j].s;

            update(base+idx,-cur);
        }

        res = max(res,xv[i]+tree[1].f+tree[1].s);

        for(int j=0;j<(int)xval[i].size();j++){
            idx = xval[i][j].f;
            cur = xval[i][j].s;

            update(base+idx,cur);
        }
    }

    base = 1;

    for(;base<=xmx;base<<=1);

    for(int i=0;i<=xmx;i++){
        tree[i+base] = pii(xv[i],0);
    }

    for(int i=xmx+1;i<base;i++){
        tree[i+base] = pii(0,0);
    }

    for(int i=base-1;i>=1;i--){
        if(tree[(i<<1)].f>tree[(i<<1)|1].f){
            tree[i].f = tree[(i<<1)].f;
            tree[i].s = max(tree[(i<<1)].s,tree[(i<<1)|1].f);
        }
        else {
            tree[i].f = tree[(i<<1)|1].f;
            tree[i].s = max(tree[(i<<1)|1].s,tree[(i<<1)].f);
        }
    }

    for(int i=0;i<=ymx;i++){
        for(int j=0;j<(int)yval[i].size();j++){
            idx = yval[i][j].f;
            cur = yval[i][j].s;

            update(base+idx,-cur);
        }

        res = max(res,yv[i]+tree[1].f+tree[1].s);

        for(int j=0;j<(int)yval[i].size();j++){
            idx = yval[i][j].f;
            cur = yval[i][j].s;

            update(base+idx,cur);
        }
    }

    cout<<res<<"\n";

    return 0;
}

E. 가위바위보 정렬

문제 설명은 역시 생략한다.

우선 $O(NT)$ 의 알고리즘으로는 당연히 시간내에 돌아가게 할 수 없다.

하지만 특수한 경우를 생각해보면, 3가지 모두 있는 케이스가 아니라 특정 2가지 종류만 있는 케이스에 대해선 답을 알아낼 수 있다.

이 경우는 같은 카드끼리 묶은 후, 횟수와 묶음의 개수에 따라서 적절히 답을 계산 가능하다. (코드 참고)

이제 3가지 경우가 다 있는 케이스가 문제인데, 이 경우는 위 처럼 2가지 경우만 있는 배열 몇개로 분할이 가능하다는 것을 보임으로써 해결 가능하다.

앞에서부터 배열($A$)을 본다고 할 때, 3가지 경우 (가위,바위,보)가 전부 나오는 최초의 시점을 생각하자. (그 지점을 $i$라고 한다.)

그럼 $A[1…(i-1)]$과 $A[i…]$가 섞이지 않는다는 것을 증명할 수 있다. 자세한 증명은 연습으로 남긴다.

그럼 이제 2가지 경우만 있는 배열 몇 개로 전체 배열을 분할 할 수 있고 (마지막 배열의 경우 1가지만 있을 수 있다.)

각각에 대해서 답을 계산해주면 원하는 답을 얻을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 5e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

pii A[MAXN];

char val[10] = {'S','R','P'};

char S[MAXN];
char T[MAXN];

int curidx = 0;

void solve(int a,int b,int k){

    if(a==b){

        for(int j=1;j<=A[a].s;j++){
            T[curidx+j] = val[A[a].f];
        }
        curidx+=A[a].s;

        return;
    }

    int va = A[a].f;
    int vb = A[a+1].f;
    
    int wv = 0;

    if(((va+1)%3) == vb){
        wv = vb;
    }
    else {
        wv = va;
    }

    int cnt = 0;

    int cur = 0;
    int ccal = 0;

    for(int i=a;i<=b;i++){

        cur = A[i].f;
        ccal = A[i].s;

        if(cur^wv){
            for(int j=1;j<=ccal;j++){
                T[curidx+j] = val[cur];
            }
            curidx+=ccal;
        }
        else {

            if(cnt>=k){
                for(int j=1;j<=ccal;j++){
                    T[curidx+j] = val[cur];
                }
                curidx+=ccal;
            }
            else if(cnt+ccal>=k){
                for(int j=1;j<=(cnt+ccal)-k;j++){
                    T[curidx+j] = val[cur];
                }
                curidx += (cnt+ccal)-k;

                cnt = k;
            }
            else {
                cnt += ccal;
            }
        }
    }

    for(int j=1;j<=cnt;j++){
        T[curidx+j] = val[wv];
    }
    curidx+=cnt;

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>k;

    cin>>S+1;

    cnt = 1;
    idx = 0;

    for(int i=2;i<=n;i++){
        if(S[i]==S[i-1]){
            cnt++;
        }
        else {
            idx++;
            if(S[i-1]=='S'){
                A[idx] = pii(0,cnt);
            }
            else if(S[i-1]=='R'){
                A[idx] = pii(1,cnt);
            }
            else {
                A[idx] = pii(2,cnt);
            }

            cnt = 1;
        }
    }

    idx++;
    if(S[n]=='S'){
        A[idx] = pii(0,cnt);
    }
    else if(S[n]=='R'){
        A[idx] = pii(1,cnt);
    }
    else {
        A[idx] = pii(2,cnt);
    }


    int bi = 0;
    int pre = 1;

    for(int i=1;i<=idx;i++){
        cur = A[i].f;
        if((bi|(1<<cur))==7){
            solve(pre,i-1,k);
            pre = i;
            bi = (1<<cur);
        }
        else {
            bi|=(1<<cur);
        }
    }

    solve(pre,idx,k);

    cout<<T+1<<"\n";

    return 0;
}

F. 간단한 문제

제목 처럼 (알고 보면) 간단한 문제 이다.

우선 두 정수 $x,y$에 대해 다음 성질이 성립한다는 것은 자명하다.

$x+y = min(x,y)+max(x,y)$ 그러므로, 문제에서 구해야 하는 식을 다음과 같이 변경 시키는 것이 가능하다.

$min({\left\lvert {p_{i}-p_{j}} \right\rvert},{\left\lvert {q_{i}-q_{j}} \right\rvert}) = ({\left\lvert {p_{i}-p_{j}} \right\rvert}+{\left\lvert {q_{i}-q_{j}} \right\rvert})-max({\left\lvert {p_{i}-p_{j}} \right\rvert},{\left\lvert {q_{i}-q_{j}} \right\rvert})$

$min$에서 $max$로 바뀐 것이 무슨 의미가 있냐고 생각할 수 있지만, 중요한 의미가 있다.

일반적으로 두 점 $(a,b)$와 $(x,y)$에 대해서 $dist = {\left\lvert {a-x} \right\rvert}+{\left\lvert {b-y} \right\rvert}$로 거리를 정의하면, $a_{1} = (a+b), b_{1} = (a-b), x_{1} = (x+y), y_{1} = (x-y)$라고 했을 때, $dist = max({\left\lvert {a_{1}-x_{1}} \right\rvert},{\left\lvert {b_{1}-y_{1}} \right\rvert})$라는 성질이 성립한다. (이에 대한 더 자세한 내용을 알고 싶으면 택시 기하를 검색해보기 바란다.)

그렇다면 이제 위의 성질을 알고 있으니, 주어진 식의 변형에서 max에 관련된 식을 다시 절댓값의 합으로 풀어줄 수 있다.

풀어주면 그걸 계산하는 건 간단한 정렬을 통해서 계산 가능하다. 하지만 대회 중엔 위의 성질을 통해 식만 변형하고, 세그 트리를 통해 복잡하게 풀었다….

아래의 코드는 나중에 작성한 간단한 풀이의 코드. 복잡한 코드는 이 문제를 맞으면 내 제출현황에서 볼 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e6+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int B[MAXN];

ll val[MAXN];

ll getans(int n)
{
    sort(val+1,val+n+1);

    ll res = 0;
    ll tot = 0;
    ll curv = 0;

    for(int i=1;i<=n;i++){
        tot += val[i];
    }

    for(int i=1;i<=n;i++){
        curv += val[i];

        res += (i*val[i]-curv);
        res += ((tot-curv)-(n-i)*val[i]);
    }

    return res;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>A[i];
    }

    for(int i=1;i<=n;i++){
        cin>>B[i];
    }

    ll res = 0;
    ll totv = 0;
    ll vv = 0;

    for(int i=1;i<=n;i++){
        val[i] = A[i];
    }

    totv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = B[i];
    }

    totv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = (A[i]+B[i]);
    }

    vv += getans(n);

    for(int i=1;i<=n;i++){
        val[i] = (A[i]-B[i]);
    }

    vv += getans(n);

    vv>>=1;

    res = totv-vv;

    cout<<res<<"\n";

    return 0;
}

H. 봉화대

문제 설명은 생략.

dp를 생각해보자. $dp[i]$를 $i$번째 봉우리까지 생각할 때 구간을 나누는 개수라고 생각하자.

현재 봉우리의 높이가 $1$이상 $N$ 이하의 서로 다른 정수이므로, $id[i]$를 높이가 $i$인 봉우리의 위치로 정의하고, $mxv[i]$를 $1$번째 봉우리 부터 $i$번째 봉우리까지의 높이 중 최댓값으로 정의하자.

$dp[i]$를 계산하기 위해 $i$번째 봉우리가 속하는 구간을 살펴보면 $id[mxv[i]]$번째 봉우리와 무조건 같은 구간에 속해야 한다는 것을 알 수 있다. 그리고, 저 봉우리와 같은 구간에 속하기만 한다면, 적어도 $i$번째 봉우리가 속하는 구간은 문제가 없다. 그러므로, $psum[i]$를 $dp[i]$의 누적합으로 정의한다면, $dp[i] = psum[id[mxv[i]]-1]$라는 등식이 성립함을 알 수 있다.

전처리에 $O(n)$, $dp$값 계산에 $O(n)$만에 계산이 가능하므로, 총 복잡도는 $O(n)$이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 5e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int id[MAXN];
int mxv[MAXN];
int dp[MAXN];
int psum[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>x;
        id[x] = i;
        A[i] = x;
    }

    for(int i=1;i<=n;i++){
        mxv[i] = max(mxv[i-1],A[i]);
    }

    dp[0] = 1;
    psum[0] = 1;

    for(int i=1;i<=n;i++){
        mx = mxv[i];
        idx = id[mx];

        dp[i] = psum[idx-1];

        psum[i] = psum[i-1]+dp[i];

        if(psum[i]>=MOD)psum[i]-=MOD;
    }

    cout<<dp[n]<<"\n";


    return 0;
}

여담: 블로그 글 처음에는 연습 이미지 순서가 잘못 돼 있었는데, jwvg0425님의 도움으로 빠르게 고칠 수 있었다. thanks in advance.

더 읽어보기 »

작성일 | In |

들어가기 전에

어제 UCPC 2021이 본선까지 모두 끝났다. 예선은 더 전인 7월 31일에 끝났지만, 후기를 쓴다는 걸 까먹어서, 대략적인 후기와 풀이를 같이 올리기로 결정했다.

팀을 구성할 때의 이야기를 잠시 하면, 나름 고등학교 부터 PS를 했지만, 서울대 소속으로 ICPC 본선에 나가는 벽은 너무도 높았다. 작년에도 꽤 강한 팀이었고, 예선 때의 컨디션도 좋았지만, 본선에 나가는데 실패했다. 올해에는 반드시 regional 본선에 가고 싶었기 때문에, 강한 팀을 만들고 싶었다. 그래서 팀원을 비교적 빠른 시간부터 물색하던 중, Sait2000님께 연락해봐야겠다고 생각했고, Sait님이 제안을 수락하시면서 ICPC를 같이 하기로 했다.

그리고 UCPC 시즌이 되고, UCPC를 Sait님과 함께 나가게 되서 남은 팀원을 찾고 있었는데, 계절학교 동기인 IHHI와 연락이 닿아서 UCPC를 일단 같이 하기로 했고, 팀연습을 진행하면서 합이 잘 맞아서 ICPC도 같이 하기로 결정했다.

UCPC 예선의 경우 각자 사정으로 따로 치되, discord를 활용해서 소통하기로 하였다. 두 번 정도의 예선 연습을 했다.

팀연습의 결과가 꽤 괜찮았고, 멤버들의 실력도 좋았기 때문에, 예선을 무난하게 통과하리라 기대하며 대회를 준비했다.

대회 진행 과정

팀연습에서 했던 대로 문제 셋을 적당히 3등분에 가깝게 나눠서 처음 문제들은 내가, 중간 문제는 Sait님이, 마지막은 IHHI가 보는 식으로 분할 했다.

총 10문제 였기 때문에 4 - 3 - 3으로 분할 했다.

A를 읽어보니 쉬운 문제 여서 빠르게 구현 후 AC. - 7분 경

B를 읽고 구현하고 있던 중 그리고 IHHI 가 H를 읽고 AC. - 15분 경

Sait님이 G를 2틀 하시고 AC. - 16분 경

이때의 2틀이 대회에서 유일한 AC 외의 결과 였다.

그리고 얼마 안 지나서 내가 B를 구현한 후 맞아서 AC. - 16분 경

여담으로, 이 시점에서 1위를 기록하고 있었다.

C를 읽었는데, 기댓값이라서 일단 넘기고 D를 고민했다.

D를 계속 고민하고 있던 중, 나머지 팀원들도 각자 맡은 문제 읽는게 끝났다.

Sait님이 I를 보고 싶어 하셨고, E가 쉬운 듯 생각이 잘 안 나신 다고 해서 IHHI에게 넘겼다.

C를 빨리 봐야 할 것 같아서 Sait님에게 봐달라고 부탁했고, Sait신이 빠르게 구현해서 맞았다. - 29분 경

C를 AC 받은 후, 난 계속 D를 고민하고, Sait님은 I를, IHHI는 E를 잡았다.

D를 고민해도 계속 안 풀려서, 잠시 점검을 했는데 J가 트리 관련 문제란 제보를 받고

읽어 보기로 했다. 보고 centroid군… 하면서 내가 잡기로 했다.

J로 가기 전에 D에 관한 관찰을 남겨놓고, J를 구현하러 갔다.

그리고 좀 있다가 Sait신이 I를 구현해서 맞았다. - 57분 경

얼마 안 있다가 IHHI가 E를 구현해서 맞았다 - 1시간 3분 경

내가 J를 계속 구현 중이었고, D가 꽤 풀리는 것 같아서 빨리 해치워야 할 것 같았기 때문에, IHHI에게 고민해달라고 부탁했다.

그런데 Sait님이 proof by ac 풀이를 떠올렸고, IHHI가 풀이를 듣고 맞는 것 같다! 라고 해서, 일단 구현. proof by AC 성공 - 1시간 14분 경

이제 남은 문제가 F, J 밖에 없었기 때문에 Sait님과 IHHI는 F를 잡았고, 난 J를 계속 구현했다.

J구현을 마치고 예제가 나왔기 때문에 일단 제출. AC - 1시간 27분 경

이때 Sait님과 IHHI는 F 풀이를 거의 완성하고 있었다. 그리고 그렇게 구한 풀이를 각자 구현 하기로 하였다. 난 풀이를 정확히 이해하는데 좀 애를 먹고, 좀 늦게 구현 하다가 Sait신이 AC - 1시간 55분 경

이렇게 대회 시작 후 2시간이 되기 전에 올솔브를 했고, 남은 시간은 팀연습 마치고 할 때 처럼 A 부터 순서대로 푼 사람이 풀이를 설명하고 토의 하는 시간을 가졌다.

그렇게 풀이를 다 말하고 나니까 어느 새 예선이 거의 끝나 있었다.

휴식을 취하면서 gravekper님의 방송을 시청하고 있었고, 스코어보드 까는 것을 지켜봤다.

결과는 아래와 같이 무려 4위.

전체적으로 굉장히 좋았다고 생각한다. Sait님이 나와 IHHI가 껄끄러워 하는 구현을 빠르게 처리해주셨고, IHHI도 E를 처리 해주었다. 그리고 나도 J를 처리해서 각자가 어느 정도 역할을 했다

Sait신이 캐리 했다는 것을 부정할 수 없지만, 나머지 팀원들도 0.7인분은 했다는 것이 내 생각이다.

결과도 4위로 무척이나 좋았다.

솔직히 대회 치기 전엔 잘하는 팀이 워낙 많아서, 말 그대로 무난히 본선 가는 정도로 예상했는데 4위를 기록해서 무척이나 기쁘기도 하고, 놀라기도 했다.

결과를 보고 운이 따라준다면 진지하게 UCPC에서도 상을 딸 수 있을 것이라 생각하게 됐다.

문제 풀이 및 구현

아래는 각 문제의 풀이다. 대회가 끝나고 업솔빙을 진행했고, I를 제외한 모든 문제를 풀었다.

I는 나중에 따로 올리던지, 여기에 추가하던지 할 예정이다.

A. 수학은 체육과목 입니다 3

수의 범위가 작으므로 (1이상 999이하) 모든 시작 수에 대해서 다 해봐도 시간 안에 무리 없이 돌아간다.

시작 수를 정해 놓고, 계속 문자열과 매치 시켜가면서 해당 시작 수에 대해 정확하게 매치되는 끝 수가 있는지 확인만 해주면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

int solve(int n,int x){

    int idx = 0;

    int a,b,c;

    int res = -1;

    for(int i=x;;i++){

        if(i>=1000){
            res = -1;
            break;
        }
        a = (i/100);
        b = (i/10)%10;
        c = (i%10);

        if(a){
            if(idx+3>n){
                res = -1;
                break;
            }
            else if(A[idx]==a&&A[idx+1]==b&&A[idx+2]==c){
                idx += 3;
                if(idx==n){
                    res = i;
                    break;
                }
            }
            else {
                res = -1;
                break;
            }
        }
        else if(b){
            if(idx+2>n){
                res = -1;
                break;
            }
            else if(A[idx]==b&&A[idx+1]==c){
                idx += 2;
                if(idx==n){
                    res = i;
                    break;
                }
            }
            else {
                res = -1;
                break;
            }
        }
        else {
            if(idx+1>n){
                res = -1;
                break;
            }
            else if(A[idx]==c){
                idx++;
                if(idx==n){
                    res = i;
                    break;
                }
            }
            else {
                res = -1;
                break;
            }
        }
    }

    return res;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>S;

    n = strlen(S);

    for(int i=0;i<n;i++){
        A[i] = S[i]-'0';
    }

    int idy = -1;

    for(int i=1;i<=999;i++){
        cur = solve(n,i);
        if(cur!=-1){
            idx = i;
            idy = cur;
            break;
        }
    }
    cout<<idx<<" "<<idy<<"\n";

    return 0;
}

B. 항체 인식

먼저 이전과 이후에서 달라진 부분이 없으면 그냥 YES이다.

달라진 부분이 하나라도 있으면, 그 셀을 X 라고 하자. X가 이전에는 a,이후에는 b 값을 가진다면, 그 셀과 같은 수(a)를 가지면서 상하좌우 이동을 통해 이동 가능한 모든 셀에 대해 그 값을 b로 바꾼다.

이제 다시 이전과 이후를 비교해서 다른게 하나라도 있는지 판별한다.

없다면, YES이다. 같으면 NO가 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<pii> que;

int A[110][110];
int B[110][110];
bool vis[110][110];

int gx[10] = {-1,0,0,1};
int gy[10] = {0,-1,1,0};

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1,idy = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>A[i][j];
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>B[i][j];
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(A[i][j]^B[i][j]){
                idx = i;
                idy = j;
                break;
            }
        }
        if(idx!=-1)break;
    }

    if(idx==-1){
        cout<<"YES\n";
        return 0;
    }

    vis[idx][idy] = true;
    cur = A[idx][idy];

    que.push(pii(idx,idy));

    while(!que.empty()){

        x = que.front().f;
        y = que.front().s;
        que.pop();

        for(int i=0;i<4;i++){
            a = x+gx[i];
            b = y+gy[i];

            if(a<0||a>n)continue;
            if(b<0||b>m)continue;

            if(vis[a][b])continue;
            if(A[a][b]^cur)continue;

            vis[a][b] = true;

            que.push(pii(a,b));
        }

    }

    int curv = B[idx][idy];

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(vis[i][j])A[i][j] = curv;
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(A[i][j]^B[i][j])cnt++;
        }
    }

    if(cnt)cout<<"NO\n";
    else cout<<"YES\n";


    return 0;
}

C. 헤이카카오

우선 $a$ 는 신경 쓸 필요 없다. 마지막에 $a$를 곱해주면 된다.

$d,k$ 가 중요하다.

$F(d,k)$가 한 판에 진행되는 시간이 1일 때, 끝말잇기를 진행하는 시간의 기댓값을 반환한다고 하면,

$d \geq 100$ 일 때, $F(d,k) = 1$이다. $d < 100$일 때, $F(d,k) = d/100 + (1-d/100)F(d+dk/100,k)$이 성립한다.

이 점화식을 그대로 구현하면 된다. 시간초과가 날 것이라 걱정할 수 있지만, 무난히 돌아간다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

double solve(double d,double k){

    if(d>=1.0){
        return 1.0;
    }

    double res = d;
    double curv = (double)1.0+solve(d*((double)1.0+k),k);

    res += ((double)1.0-d)*curv;

    return res;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>a>>x>>y;

    double dd = (double)x/(double)100.0;
    double kk = (double)y/(double)100.0;



    double res = solve(dd,kk);

    res*=(double)a;

    cout<<fixed;
    cout.precision(15);

    cout<<res<<"\n";

    return 0;
}

D. 돌 가져가기

일단 관찰할 수 있는 것은, 색깔이 같으면서 연속된 것들을 생각하면, 그 중에 하나만 점수를 얻을 수 있다. 따라서 압축한 후 그 중의 최댓값들만 고려해도 무방하다.

그리고 또 하나는, 양 쪽 끝에 있는 것들은 가져갈 수 없다.

그리고 마지막 관찰은, 가져가는 개수가 정해져 있다는 것이다.

정확히 양 끝을 제외하고 $k$개의 값을 고려한다면, $k = 2m$이면 $m$, $k = 2m+1$이면 $m+1$개를 가져간다. $a$개를 가져 간다고 하면, $k$ 개의 값 중 가장 큰 $a$개의 수들의 합 보다 답이 클 수 없다는 것을 알 수 있다.

그리고 위와 같이 가져가는 방법이 존재하며, 이 내용을 구현하면 맞는다.

자세한 증명은 풀이 슬라이드 참조.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 3e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    cin>>S+1;

    for(int i=1;i<=n;i++){
        cin>>A[i];
    }

    vector<int> val;

    S[0] = S[1];

    mx = 0;

    for(int i=1;i<=n;i++){
        if(S[i]^S[i-1]){
            val.push_back(mx);
            mx = A[i];
        }
        else {
            mx = max(mx,A[i]);
        }
    }

    val.push_back(mx);

    vector<int> rval;

    int vsz = (int)val.size();

    for(int i=1;i<vsz-1;i++){
        rval.push_back(val[i]);
    }

    sort(rval.begin(),rval.end(),greater<int>());

    int rsz = (int)rval.size();

    m = (rsz+1)>>1;

    ll res = 0;

    for(int i=0;i<m;i++){
        res += (ll)rval[i];
    }

    cout<<res<<"\n";

    return 0;
}

E. 말뚝

우선 할 수 있는 관찰은, 정확히 연속한 $K$개의 높이를 같게 하는 값을 계산해도 된다는 것이다. 이상으로 하면 비용이 더 많이 들었으면 들었지 줄지 않으니까.

그리고 어떤 말뚝에 대해서 조정하는 높이에 따른 비용 함수의 그래프를 그리면, 절댓값 함수와 비슷한 개형의 꺽은선 그래프가 됨을 알 수 있다.

따라서 비용 함수 몇 개를 합한 것을 생각하면, 볼록한 모양임을 알 수 있다. 정확히는 직선 여러개가 이어져 있는데, 기울기가 x 좌표가 커질 수록 증가하는 형태가 된다. 따라서, 어떤 점 x에 대해 x이상인 좌표들에 대해서 그 기울기가 음이 아닌 최소의 지점을 찾고, 그 지점에서의 비용을 구하면 된다는 것을 알 수 있다. 이건 삼분탐색이나, 이분탐색으로 빠르게 찾을 수 있고, 함수의 추가와 삭제를 빠르게 하기 위햇 세그트리 등을 이용한다. 난 세그 트리 (인덱스 트리 ) + 이분탐색으로 구현했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
int B[MAXN];
int H[MAXN];
char S[MAXN];

ll atree[MAXN*4];
ll btree[MAXN*4];
ll axtree[MAXN*4];
ll bxtree[MAXN*4];

inline void update(int tmp,int a,int b,int x){

    atree[tmp]+=(ll)a;
    btree[tmp]+=(ll)b;
    axtree[tmp]+=(1LL*a*x);
    bxtree[tmp]+=(1LL*b*x);
    tmp>>=1;

    while(tmp){
        atree[tmp] = atree[(tmp<<1)]+atree[(tmp<<1)|1];
        btree[tmp] = btree[(tmp<<1)]+btree[(tmp<<1)|1];
        axtree[tmp] = axtree[(tmp<<1)]+axtree[(tmp<<1)|1];
        bxtree[tmp] = bxtree[(tmp<<1)]+bxtree[(tmp<<1)|1];
        tmp>>=1;
    }

    return;
}

inline ll getans(int base){

    int tmp = 1;

    ll va = 0;
    ll vb = 0;
    ll vax = 0;
    ll vbx = 0;

    while(tmp<base){

        if(va+atree[(tmp<<1)]>=vb+btree[(tmp<<1)|1]){
            vb += btree[(tmp<<1)|1];
            vbx += bxtree[(tmp<<1)|1];
            tmp<<=1;
        }
        else {
            va += atree[(tmp<<1)];
            vax += axtree[(tmp<<1)];
            tmp<<=1;
            tmp|=1;
        }
    }

    ll idx = (tmp-base);

    ll res = (idx*va-vax)+(vbx-idx*vb);

    return res;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>k;

    for(int i=1;i<=n;i++){
        cin>>H[i];
        mx = max(mx,H[i]);
    }

    for(int i=1;i<=n;i++){
        cin>>A[i];
    }

    for(int i=1;i<=n;i++){
        cin>>B[i];
    }

    int base = 1;

    for(;base<=mx;base<<=1);

    for(int i=1;i<=k;i++){
        update(base+H[i],A[i],B[i],H[i]);
    }

    ll res = getans(base);

    for(int i=k+1;i<=n;i++){
        update(base+H[i],A[i],B[i],H[i]);
        update(base+H[i-k],-A[i-k],-B[i-k],H[i-k]);

        res = min(res,getans(base));
    }

    cout<<res<<"\n";

    return 0;
}

F. 종이, 펜, 삼각형

일단 한 점에서 동시에 만나는게 아닌 이상, 충분히 큰 평면에 대해서는 정삼각형을 이룬다는 것을 알 수 있다. 문제는 그것이 기존의 큰 정삼각형 안에 들어가야 한다는 것이다.

편의상 직선의 기울기가 커지는 순서대로 $a$방향, $b$방향, $c$방향이라 하자. 그리고 기존에 있었던 $a$방향, $b$방향, $c$방향 직선 (큰 정삼각형을 이루는 직선들)을 $a0,b0,c0$이라 하자. 그럼 다음과 같은 경우로 나누어 개수를 셀 수 있다.

  • 기존의 큰 정삼각형
  • $a0$와 $b,c$ 방향 직선이 이루는 정삼각형
  • $b0$와 $a,c$ 방향 직선이 이루는 정삼각형
  • $c0$와 $a,b$ 방향 직선이 이루는 정삼각형
  • $a0,b0$와 $c$ 방향 직선이 이루는 정삼각형
  • $b0,c0$와 $a$ 방향 직선이 이루는 정삼각형
  • $a0,c0$와 $b$ 방향 직선이 이루는 정삼각형
  • $a,b,c$ 방향 직선이 이루는 정삼각형

$a,b,c$ 방향 직선이 이루는 정삼각형의 경우를 제외하면 정렬과 세그 트리 등을 이용해 세 줄 수 있다. $a,b,c$ 방향 직선이 이루는 정삼각형의 경우, 세그 트리를 통해서 세어주되, 세 직선이 한 점에서 만나는 경우를 고려해주어야 한다. 이는 fft를 통해 풀 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

namespace fft{

typedef complex<double> base;
void fft(vector<base> &a, bool inv){
	int n = a.size(), j = 0;
	vector<base> roots(n/2);
	for(int i=1; i<n; i++){
		int bit = (n >> 1);
		while(j >= bit){
			j -= bit;
			bit >>= 1;
		}
		j += bit;
		if(i < j) swap(a[i], a[j]);
	}
	double ang = 2 * acos(-1) / n * (inv ? -1 : 1);
	for(int i=0; i<n/2; i++){
		roots[i] = base(cos(ang * i), sin(ang * i));
	}
	/* In NTT, let prr = primitive root. Then,
	int ang = ipow(prr, (mod - 1) / n);
	if(inv) ang = ipow(ang, mod - 2);
	for(int i=0; i<n/2; i++){
		roots[i] = (i ? (1ll * roots[i-1] * ang % mod) : 1);
	}
	XOR Convolution : set roots[*] = 1.
	OR Convolution : set roots[*] = 1, and do following:
    if (!inv) {
        a[j + k] = u + v;
        a[j + k + i/2] = u;
    } else {
        a[j + k] = v;
        a[j + k + i/2] = u - v;
    }
	*/
	for(int i=2; i<=n; i<<=1){
		int step = n / i;
		for(int j=0; j<n; j+=i){
			for(int k=0; k<i/2; k++){
				base u = a[j+k], v = a[j+k+i/2] * roots[step * k];
				a[j+k] = u+v;
				a[j+k+i/2] = u-v;
			}
		}
	}
	if(inv) for(int i=0; i<n; i++) a[i] /= n; // skip for OR convolution.
}

vector<ll> multiply(vector<ll> &v, vector<ll> &w){
	vector<base> fv(v.begin(), v.end()), fw(w.begin(), w.end());
	int n = 2; while(n < v.size() + w.size()) n <<= 1;
	fv.resize(n); fw.resize(n);
	fft(fv, 0); fft(fw, 0);
	for(int i=0; i<n; i++) fv[i] *= fw[i];
	fft(fv, 1);
	vector<ll> ret(n);
	for(int i=0; i<n; i++) ret[i] = (ll)round(fv[i].real());
	return ret;
}
vector<ll> multiply(vector<ll> &v, vector<ll> &w, ll mod){
	int n = 2; while(n < v.size() + w.size()) n <<= 1;
	vector<base> v1(n), v2(n), r1(n), r2(n);
	for(int i=0; i<v.size(); i++){
		v1[i] = base(v[i] >> 15, v[i] & 32767);
	}
	for(int i=0; i<w.size(); i++){
		v2[i] = base(w[i] >> 15, w[i] & 32767);
	}
	fft(v1, 0);
	fft(v2, 0);
	for(int i=0; i<n; i++){
		int j = (i ? (n - i) : i);
		base ans1 = (v1[i] + conj(v1[j])) * base(0.5, 0);
		base ans2 = (v1[i] - conj(v1[j])) * base(0, -0.5);
		base ans3 = (v2[i] + conj(v2[j])) * base(0.5, 0);
		base ans4 = (v2[i] - conj(v2[j])) * base(0, -0.5);
		r1[i] = (ans1 * ans3) + (ans1 * ans4) * base(0, 1);
		r2[i] = (ans2 * ans3) + (ans2 * ans4) * base(0, 1);
	}
	fft(r1, 1);
	fft(r2, 1);
	vector<ll> ret(n);
	for(int i=0; i<n; i++){
		ll av = (ll)round(r1[i].real());
		ll bv = (ll)round(r1[i].imag()) + (ll)round(r2[i].real());
		ll cv = (ll)round(r2[i].imag());
		av %= mod, bv %= mod, cv %= mod;
		ret[i] = (av << 30) + (bv << 15) + cv;
		ret[i] %= mod;
		ret[i] += mod;
		ret[i] %= mod;
	}
	return ret;
}
}

vector<int> A;
vector<int> B;
vector<int> C;

int AA[MAXN];
int BB[MAXN];
int CC[MAXN];

int tree[MAXN*4];

void update(int tmp){

    while(tmp){
        tree[tmp]++;
        tmp>>=1;
    }

    return;
}

int getans(int L,int R){

    int res = 0;

    while(L<=R){
        if(L&1){
            res += tree[L];
            L++;
        }
        if(!(R&1)){
            res += tree[R];
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}


int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>m>>q;

    for(int i=0;i<q;i++){
        cin>>a>>x;

        if(a==0){
            B.push_back(x);
        }
        else if(a==60){
            C.push_back(x);
        }
        else {
            A.push_back(x);
        }
    }

    sort(A.begin(),A.end());
    sort(B.begin(),B.end());
    sort(C.begin(),C.end());

    ll res = 1+q;

    int asz = (int)A.size();

    for(int i=0;i<asz;i++){

        idx = lower_bound(B.begin(),B.end(),A[i])-B.begin();
        res += (ll)idx;

        idx = lower_bound(C.begin(),C.end(),A[i])-C.begin();
        res += (ll)idx;
    }

    int bsz = (int)B.size();
    int csz = (int)C.size();

    for(int i=0;i<bsz;i++){
        idx = lower_bound(C.begin(),C.end(),m-B[i])-C.begin();
        res += (ll)idx;
    }

    for(int i=0;i<asz;i++){
        AA[A[i]] = 1;
    }

    for(int i=0;i<bsz;i++){
        BB[B[i]] = 1;
    }

    for(int i=0;i<csz;i++){
        CC[C[i]] = 1;
    }

    int base = 1;

    for(;base<m;base<<=1);

    ll curv = 0;

    for(int i=1;i<m;i++){

        if(CC[i]){
            update(base+i);
        }

        if(BB[i]){
            curv += (ll)getans(base,base+m-i);
        }

        if(AA[i]){
            res += curv;
        }
    }

    fill(tree,tree+(base<<1),0);

    curv = 0;

    for(int i=1;i<m;i++){

        if(CC[i]){
            curv += (ll)getans(base,base+m-i);
        }

        if(BB[i]){
            update(base+i);
        }

        if(AA[i]){
            res += curv;
        }
    }

    vector<ll> vb;
    vector<ll> vc;

    vb = vector<ll> (m);
    vc = vector<ll> (m);

    for(int i=1;i<m;i++){
        vb[i] = BB[i];
        vc[i] = CC[i];
    }

    vector<ll> vres = fft::multiply(vb,vc);

    for(int i=1;i<m;i++){
        if(AA[i]){
            res -= vres[i];
        }
    }

    cout<<res<<"\n";


    return 0;
}

G. 경품 추첨

우선 느낌상 한 상자 내에선 규칙적으로 배열해야 할 것 같다. 수들이 등차수열이라고 하자. 어떤 상자 $a,b$에 대해서, 각 상자의 공차가 $d_{a},d_{b}$라고 두면,

$d_{a} \times v_{a} = d_{b} \times v_{b}$인 $v_{a},v_{b}$가 존재하지 않도록 하고 싶다.

이는 현재 제한을 생각해보면, 각 공차들이 2000보다 큰 소수일 경우 해결된다.

2000을 넘는 소수 중 작은 것부터 공차들을 정하면 충분히 제한 내에 들어가고, 그대로 해결할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

bool is_prime(int x){

    bool judge = true;

    for(int i=2;i*i<=x;i++){
        if(!(x%i)){
            judge = false;
            break;
        }
    }

    return judge;
}

void init(int k){

    int idx = 2001;

    for(int i=0;i<k;i++){
        while(true){
            if(is_prime(idx))break;
            idx++;
        }
        A[i] = idx;
        idx++;
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>k>>n;

    init(k);

    for(int i=0;i<k;i++){

        cur = A[i];

        for(int j=1;j<=n;j++){
            cout<<j*cur<<" ";
        }
        cout<<"\n";
    }

    return 0;
}

H. 스키장

제한을 주의 깊게 보지 않으면, 일반 그래프에서 최장경로를 구하는 형태가 되므로, 풀기 어렵다. 하지만, 제한을 본다면 $K <= 10 $으로, 역행 가능 횟수가 굉장히 작음을 알 수 있다.

따라서 역행 횟수와 최장 경로 길이를 함께 저장해 나가는 dp를 하면 된다.

여담으로, IHHI가 제한을 안 보고 어렵네 하고 지나쳤다가 제한을 보고 부랴부랴 코딩했다고…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

ll dp[20][MAXN];

vector<pii> val[MAXN];
vector<int> vval[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m>>k>>a>>b;

    for(int i=0;i<m;i++){
        cin>>x>>y>>cur;
        val[x].push_back(pii(y,cur));
        vval[y].push_back(x);
    }

    for(int i=1;i<=n;i++){
        dp[0][i] = -LINF;
    }

    dp[0][b] = 0;

    for(int i=b-1;i>=1;i--){
        for(int j=0;j<(int)val[i].size();j++){
            x = val[i][j].f;
            cur = val[i][j].s;
            dp[0][i] = max(dp[0][i],dp[0][x]+(ll)cur);
        }
    }

    ll curv = -LINF;

    for(int t=1;t<=k;t++){

        for(int i=n;i>=1;i--){
            curv = -LINF;
            for(int j=0;j<(int)val[i].size();j++){
                x = val[i][j].f;
                cur = val[i][j].s;
                curv = max(curv,dp[t][x]+(ll)cur);
            }
            for(int j=0;j<(int)vval[i].size();j++){
                x = vval[i][j];
                curv = max(curv,dp[t-1][x]);
            }
            dp[t][i] = curv;
        }
    }

    ll res = dp[k][a];

    if(res<0)cout<<"-1\n";
    else cout<<res<<"\n";

    return 0;
}

I. 흔한 타일 색칠 문제

간단하게나마 풀이를 기술하면, 재귀를 통해서 해결할 수 있다.

사각형을 4등분하고, 비워져 있는 사각형을 제외한 나머지 사각형은 가운데쪽의 귀퉁이를 비우는 식으로 재귀를 하는 것.

자세한 풀이는 공식 풀이를 참고하기 바란다.

J. UCPC 만들기

centorid를 사용하는 유형이다. 결국 경로에서 $UCPC ^ {k}$꼴의 형태가 되기 위해서는, U,P의 개수가 같고, C와 나머지 문자의 개수가 서로 같으면 된다. 현재 보고 있는 트리에 대해 centroid를 root으로 하고, centroid의 자식들을 root로 하는 subtree에 대해서, 루트 부터 각 정점 까지 U,P 개수의 차와 C와 나머지 문자의 개수의 차를 함께 저장하고, 각 순서쌍이 몇 개나 있는지 저장한다. 그리고 각 subtree에 대해 자신을 제외한 나머지 subtree에서 자신이랑 합하면 두 차가 모두 0이 되는 것이 얼마나 있는지 센다. 현재 보고 있는 트리에서 해결하면, 이제 subtree에 대해서 다시 이 문제를 풀면 끝난다.

centroid에 대한 문제를 많이 풀어보면 쉽게 접근 가능한 유형.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
vector<vector<int> >ctree;
queue<int> que;

pii curval[MAXN];
vector<pii> val[MAXN];
vector<int> cal[MAXN];

int chk[MAXN];
int subtree[MAXN];
char S[MAXN];

ll ans = 0;

void dfs(int here,int p)
{
    int there;

    subtree[here] = 1;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        if(chk[there])continue;
        dfs(there,here);
        subtree[here]+=subtree[there];
    }

    return;
}

int mysearch(int here,int p,int sz)
{
    int there;
    int idx = -1;
    int mx = 0;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        if(chk[there])continue;
        if(mx<subtree[there]){
            mx = subtree[there];
            idx = i;
        }
    }

    if(idx==-1){
        return here;
    }

    if((mx<<1)<=sz)return here;

    return mysearch(graph[here][idx],here,sz);
}

int cent;

void ddfs(int here,int p){

    int there;

    if(S[here]=='U'){
        curval[here].f--;
        curval[here].s++;
    }
    else if(S[here]=='P'){
        curval[here].f--;
        curval[here].s--;
    }
    else {
        curval[here].f++;
    }

    val[cent].push_back(curval[here]);

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        if(chk[there])continue;
        curval[there] = curval[here];
        ddfs(there,here);
    }

    return;
}

int va,vb;

void getans(int here,int p){

    int there;

    int x = -curval[here].f;
    int y = -curval[here].s;

    x+=va;
    y+=vb;

    int idx = lower_bound(val[cent].begin(),val[cent].end(),pii(x,y))-val[cent].begin();

    if(idx<(int)val[cent].size()){
        if(val[cent][idx].f==x&&val[cent][idx].s==y){
            ans += (ll)cal[cent][idx];
        }
    }

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        if(chk[there])continue;
        getans(there,here);
    }

    return;
}


void update(int here,int p){

    int there;

    int idx = lower_bound(val[cent].begin(),val[cent].end(),curval[here])-val[cent].begin();
    cal[cent][idx]++;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        if(chk[there])continue;
        update(there,here);
    }

    return;
}

void solve(int here,int sz,int num)
{
    if(sz==1){
        chk[here] = num;
        return ;
    }

    dfs(here,0);

    int res = mysearch(here,0,sz);

    chk[res] = num;

    cent = res;

    curval[res] = pii(0,0);

    ddfs(res,0);

    sort(val[res].begin(),val[res].end());
    val[res].erase(unique(val[res].begin(),val[res].end()),val[res].end());

    int vsz = (int)val[res].size();

    cal[res] = vector<int> (vsz);

    int idx = lower_bound(val[res].begin(),val[res].end(),curval[res])-val[res].begin();
    cal[res][idx]++;

    if(S[res]=='U'){
        va = -1;
        vb = 1;
    }
    else if(S[res]=='P'){
        va = -1;
        vb = -1;
    }
    else {
        va = 1;
        vb = 0;
    }

    int there;

    for(int i=0;i<graph[res].size();i++){
        there = graph[res][i];
        if(chk[there])continue;
        getans(there,res);
        update(there,res);
    }

    int nxtsz;
    int nxt;

    for(int i=0;i<graph[res].size();i++){
        there = graph[res][i];
        if(chk[there])continue;

        if(subtree[res]>subtree[there])nxtsz = subtree[there];
        else nxtsz = sz-subtree[res];

        solve(there,nxtsz,num+1);
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    cin>>S+1;

    graph = vector<vector<int> > (n+1);
    ctree = vector<vector<int> > (n+1);

    for(int i=1;i<n;i++){
        cin>>x>>y;
        graph[x].push_back(y);
        graph[y].push_back(x);
    }

    solve(1,n,1);

    cout<<ans<<"\n";

    return 0;
}
더 읽어보기 »

작성일 | In |

결과 및 총평

내 제출현황과 순위는 위와 같다.

참가하기 전에 컨디션이 별로 였는데 이 정도면 훌륭하게 마친 것 같아 개인적으론 만족스럽다. A~D를 모두 거의 막힘 없이 적당히 밀었다. D에서 WA가 난 건 조금만 고민하면 한번에 AC가 가능했을 것 같아서 아까웠다.

문제는 여기에서 확인이 가능하다.

A~D에 대한 간단한 풀이, 리뷰, 코드이다.

A. LR Constraints

처음 읽었을 땐 살짝 당황했던 문제.

먼저 $N < K$일 경우 $0$이 됨은 쉽게 알아낼 수 있다.

그러므로 $N \leq K$인 경우만 생각한다.

우선 조건에 의해서 모든 $k_i$가 다르다. 그러므로 특정 위치에 대해선 써야 하는 수가 정해진다. 그리고 leftmost혹은 rightmost이어야 하므로, 어떤 수 $i$를 쓸 수 있는 범위가 정해진다. 따라서 해당 범위에 쓸 수 있는 수를 +1 해주고, 모든 위치에 써야하는 수가 정해지지 않았다면 쓸 수 있는 수의 개수를 곱해주면 된다.

별로 어렵지 않은 문제였는데도 시간을 약간 쓴 것 같다…

코드는 다음과 같다. 내 코드의 시간 복잡도는 $O(kn)$이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

int cal[MAXN];

bool chk[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    char c;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>k;

    for(int i=1;i<=k;i++){
        cin>>c>>x;
        if(c=='L')A[i] = (x<<1);
        else A[i] = (x<<1)|1;
    }

    if(n<k){
        cout<<0<<"\n";
        return 0;
    }

    for(int i=1;i<=k;i++){

        cur = (A[i]>>1);

        chk[cur] = true;

        if(A[i]&1){
            for(int j=1;j<cur;j++){
                cal[j]++;
            }
        }
        else {
            for(int j=cur+1;j<=n;j++){
                cal[j]++;
            }
        }

    }

    ll res = 1;

    for(int i=1;i<=n;i++){
        if(chk[i])continue;

        res = (res*(ll)cal[i])%PMOD;

    }

    cout<<res<<"\n";


    return 0;
}

B. XOR Matching 2

내가 좋아하는 XOR 문제가 나왔다.

문제 조건은 가능하다. $a_{i}, b_{i}$들을 적당히 재배열해서, 모든 $i$에 대해서 $a_{i} \oplus b_{i}$가 같은 값이 되게 할 수 있을 때, 그 값의 개수가 몇개인지, 그리고 어떤 수들이 가능한지 구하는 문제이다.

XOR의 성질 을 이용하면, 어떤 수 $a,x$에 대해서, $a \oplus b = x$가 되는 $b$는 유일하다. 이 성질을 이용하면, 주어진 조건을 만족하는 $x$를 고정했을 때, $a_{i}$에 대해서, $b_{i}$가 유일하게 정해진다는 것이다.

그러므로, 좌표압축을 통해서 $a_{i},b_{i}$ 각각에 서로 다른 수가 몇개 있고, 각각이 서로 다른 수들에 대해 수열 내에 개수가 몇개가 되는지 저장한 배열을 전처리로 저장해둔다. $a_{i}$를 좌표압축한 결과를 $c_{j}$라하고, 비슷하게 $d_{t}$를 $b_{i}$를 압축한 결과라하면, 가능한 $x$값의 후보들은 $c_{j} \oplus d_{t}$이다. 그리고 후보들에 대해서 실제로 가능한지 알아보려면, 우선 어떤 $c_{j}$에 대해 $c_{j} \oplus x = d_{t}$인 $d_{t}$가 존재해야 한다. 그리고 $a_{i},b_{i}$내에 $c_{j},d_{t}$의 개수가 같아야만 한다. 그렇지 않다면 한쪽이 남게 되고, 그 수는 다른 수와 매칭되어 XOR한 값이 $x$가 아니게 된다. 이 조건이 모든 $c_{j}$에 대해서 성립하면, 그 $x$는 문제에서 원하는 $x$가 된다.

위의 유일성 성질 때문에, 각 $c_{j}$에 대해 특정 수 $x$에 대해 조건을 만족하는 $d_{t}$는 모두 달라지므로, 겹칠 염려는 없다.

위의 내용을 코드로 적당히 빠르게 구현하면 AC를 받을 수 있다.

내 코드의 시간 복잡도는 $O(n^{2}logn)$이다. 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 4e6+10;
const int MAXM = 2e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXM];
int B[MAXM];
int calA[MAXM];
int calB[MAXM];
int cal[MAXN];

vector<int> valA;
vector<int> valB;

vector<int> val;

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++)
        cin>>A[i];

    for(int i=0;i<n;i++)
        cin>>B[i];

    for(int i=0;i<n;i++){
        valA.push_back(A[i]);
        valB.push_back(B[i]);
    }
    sort(valA.begin(),valA.end());
    valA.erase(unique(valA.begin(),valA.end()),valA.end());

    sort(valB.begin(),valB.end());
    valB.erase(unique(valB.begin(),valB.end()),valB.end());

    int asz = (int)valA.size();
    int bsz = (int)valB.size();

    for(int i=0;i<asz;i++){
        for(int j=0;j<bsz;j++){
            val.push_back(valA[i]^valB[j]);
        }
    }

    sort(val.begin(),val.end());
    val.erase(unique(val.begin(),val.end()),val.end());

    for(int i=0;i<n;i++){
        idx = lower_bound(valA.begin(),valA.end(),A[i])-valA.begin();
        calA[idx]++;
        idx = lower_bound(valB.begin(),valB.end(),B[i])-valB.begin();
        calB[idx]++;
    }

    for(int i=0;i<asz;i++){
        for(int j=0;j<bsz;j++){
            if(calA[i]==calB[j]){
                cur = valA[i]^valB[j];
                idx = lower_bound(val.begin(),val.end(),cur)-val.begin();
                cal[idx]+=calA[i];
            }
        }
    }

    int vsz = (int)val.size();

    vector<int> ans;

    for(int i=0;i<vsz;i++){
        if(cal[i]==n){
            ans.push_back(val[i]);
        }
    }

    int sz = (int)ans.size();

    cout<<sz<<"\n";

    for(int i=0;i<sz;i++){
        cout<<ans[i]<<"\n";
    }


    return 0;
}

C. LCM of GCDs

여담으로, 2020 Yokohama regional에 같은 제목의 문제가 있다.

링크에서 확인 가능하다.

처음에는 합의 LCM인 줄 알고 삽질 하다가… 문제를 다시 읽고 풀었다.

우선 각 가방 내의 수들의 GCD의 LCM이라는 점을 생각하면, 결국 가능한 $X,Y$들의 후보는 처음에 들어갔던 수들의 약수임을 알 수 있다. 그리고, 현재 $a_{i},b_{i} \leq 1000000000$이므로, 약수의 개수가 아무리 많아봤자 $O(n^{\frac{1}{3}})$에 비례 하고 현재 범위에선 대충 $6$배 정도의 상수가 붙는 다는 것을 감안하면, 대충 $6000$개 안에 들어갈 것이라 생각할 수 있고, 따라서 쌍의 개수는 많아봤자 $36000000$개 정도일 것이다. 그리고 $N \leq 50$이므로, 4초라는 제한시간을 생각하면 $N$번 순회하면서 모든 쌍이 가능한지 dp를 통해 체크하면 시간 안에 돌것이라는 것을 알 수 있다.

만약 dp가 아니라 그리디를 쓰면 WA를 받는다고 한다. 수작업을 한 케이스가 있는 듯.

시간을 아끼기 위해서, 미리 처음 수의 약수들과 현재 수들의 gcd를 미리 계산 해두고, $X,Y$ 값은 새로운 카드를 집어 넣을 때마다 항상 증가하지 않는 다는 점을 이용해서 순회한다. 또, 미리 정렬해서 특정 케이스에서 봐야하는 쌍의 수를 약간 줄이는 (실제론 늘어날 수도 있다.) 처리를 해준다.

위의 약수의 개수에 관한 내용은

링크를 통해서 확인 가능하다.

좀 더 엄밀한 bound를 원한다면 이쪽을 참고하라.

좋은 자료를 주신 evenharder님과 rkm0959에게 감사를 표한다.

코드는 다음과 같다. 시간 복잡도는 $O(Nk^{\frac{2}{3}})$이다. 실행시간은 113ms로, 매우 빠르게 돈다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 6e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

pii A[MAXN];
char S[MAXN];

int AA[MAXM];
int AB[MAXM];
int BA[MAXM];
int BB[MAXM];

int mygcd(int a,int b){
    return a?mygcd(b%a,a):b;
}

bool chk[MAXM][MAXM];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++){
        cin>>A[i].f>>A[i].s;
        if(A[i].f>A[i].s)swap(A[i].f,A[i].s);
    }

    sort(A,A+n);

    vector<int> fac;
    vector<int> ffac;

    k = A[0].f;

    for(int i=1;i*i<=k;i++){
        if(!(k%i)){
            fac.push_back(i);
            if(i*i<k)fac.push_back(k/i);
        }
    }

    m = A[0].s;

    for(int i=1;i*i<=m;i++){
        if(!(m%i)){
            ffac.push_back(i);
            if(i*i<m)ffac.push_back(m/i);
        }
    }

    sort(fac.begin(),fac.end());
    sort(ffac.begin(),ffac.end());

    int fsz = (int)fac.size();
    int ffsz = (int)ffac.size();

    chk[fsz-1][ffsz-1] = true;

    for(int t=1;t<n;t++){

        a = A[t].f;
        b = A[t].s;

        for(int i=0;i<fsz;i++){
            cur = mygcd(a,fac[i]);
            AA[i] = lower_bound(fac.begin(),fac.end(),cur)-fac.begin();
        }

        for(int i=0;i<ffsz;i++){
            cur = mygcd(a,ffac[i]);
            AB[i] = lower_bound(ffac.begin(),ffac.end(),cur)-ffac.begin();
        }

        for(int i=0;i<fsz;i++){
            cur = mygcd(b,fac[i]);
            BA[i] = lower_bound(fac.begin(),fac.end(),cur)-fac.begin();
        }

        for(int i=0;i<ffsz;i++){
            cur = mygcd(b,ffac[i]);
            BB[i] = lower_bound(ffac.begin(),ffac.end(),cur)-ffac.begin();
        }

        for(int i=0;i<fsz;i++){

            for(int j=0;j<ffsz;j++){
                if(chk[i][j]){
                    chk[i][j] = false;
                    a = AA[i];
                    b = BB[j];
                    chk[a][b] = true;
                    a = AB[j];
                    b = BA[i];
                    chk[b][a] = true;
                }
            }
        }
    }

    ll res = 0;
    ll curv;

    for(int i=0;i<fsz;i++){
        for(int j=0;j<ffsz;j++){
            if(chk[i][j]){
                curv = 1LL*fac[i]*ffac[j];
                curv /= mygcd(fac[i],ffac[j]);
                res = max(res,curv);

            }
        }
    }

    cout<<res<<"\n";

    return 0;
}

D. Yet Another Sorting Problem

$N,M$인 조건만 없다면 굉장히 Well Known인 문제이다. 순열을 그래프로 표현했을 때, 전체 수의 개수 $K$에서 연결 컴포넌트의 개수 $C$를 뺀 $K-C$가 swap에서 제한이 없을 때의 정답이다. (여기서 순열 그래프란, permutaion $p$에 대해서, 정점 $i$에 대해 $i$에서 $p_i$로 가는 edge가 있는 그래프를 의미한다.)

하지만 이 문제에선 $1 \leq i \leq N$인 $i$와 $N+1 \leq j \leq N+M$인 $i,j$에 대해서만 swap을 진행할 수 있다는 제한 조건이 있다.

우선 원래 문제에서 swap operation이 그래프 상에서 어떤 작업과 같은지 한번 보자. 위에서 언급한 제한이 없는 경우에서, swap operation은 현재 그래프 상에서 인접한 두 indices에 대해 적용하는게 최선이다. 좀 더 formal하게 말하면, 어떤 $i$에 대해 $i$가 가리키는 정점이 $j$이면, $i,j$에 대해 swap을 적용시켜 나가는 것이 최적이다.

이 연산이 그래프 상에서 어떤 식으로 구현되는지 보면, $i,j$에서 swap을 할 때 $j$가리키는 정점을 $k$라 할 때, $j$는 이제 자기 자신을 가리키게 되고, $i$가 $k$를 가리키게 된다. 이것에 집중하면 문제를 해결할 실마리를 잡을 수 있다.

이제 다시 제한이 있는 경우로 돌아와서, 제한에 의해서 swap을 적용할 수 있는 경우는, $i$가 $N$이하이고, $j$가 $N$초과이거나, 또는 그 반대여야만 한다. 이는 그래프 상에서 인접한 정점이 한쪽은 $N$이하고, 다른 한쪽은 그렇지 않은 경우만 바꿀 수 있다는 것이다. 이 성질을 이용하면, 순열 그래프에서 어떤 연결 컴포넌트에 대해, 컴포넌트 내에서 $N$이하인 점과 $N$초과인 점이 모둔 들어 있는 컴포넌트는 변함 없이 컴포넌트 내의 정점 개수를 $A$라 하면 $A-1$번 만에 모두 해결할 수 있다.

어느 한쪽만 있는 경우가 문제 인데, 만약 컴포넌트 내의 정점 개수가 1개라면, 이미 제자리에 있으니 신경 쓰지 않아도 된다. 만약 $N$이하인 수들만 포함하고, 정점 개수가 2 이상인 컴포넌트가 $W$개, $N$초과인 수들만 있고 정점 개수가 2 이상인 컴포넌트가 $B$개 있다고 하자. 컴포넌트 내에선 정렬이 불가능하니, 적절히 병합한 후 해결해야 함을 어렵지 않게 알 수 있다. 이때, $W,B$개의 컴포넌트들을 최대한 짝지어 병합한다. 그러고 어느 한쪽이 남는다면, 아무 컴포넌트에 적절히 병합한다. 그후 정렬 시키면 답을 얻는다. 따라서 병합 시의 비용을 계산하면 되는데, 이는 코드를 참고해도 충분할 것이라 생각한다.

순열 그래프에 대한 감은 이 문제를 풀면 대략적으로 알 수 있을 것이다.

순열 그래프는 그 여러 가지 성질 때문에, 자주 나오니 공부해두자.

코드는 다음과 같다. 시간 복잡도는 $O(N+M)$이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

bool vis[MAXN];
int cycle[MAXN];
int cal[MAXN];
int bb[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>m;

    for(int i=1;i<=n+m;i++)
    {
        cin>>A[i];
    }

    int num = 0;

    for(int i=1;i<=n+m;i++){
        if(vis[i])continue;
        cnt = 0;
        cur = i;

        num++;

        while(!vis[cur]){
            vis[cur] = true;
            cycle[cur] = num;
            cnt++;
            cur = A[cur];
        }

        cal[num] = cnt;
    }

    for(int i=1;i<=n;i++){
        cur = cycle[i];
        bb[cur]|=1;
    }

    for(int i=n+1;i<=n+m;i++){
        cur = cycle[i];
        bb[cur]|=2;
    }

    int cntb = 0;
    int cntw = 0;

    int cnto = 0;
    int res = 0;

    for(int i=1;i<=num;i++){
        if(cal[i]==1)continue;
        if(bb[i]==3){
            res += (cal[i]-1);
            continue;
        }

        assert(bb[i]);

        cnto+=cal[i];

        if(bb[i]==1)cntw++;
        else cntb++;
    }

    cur = max(cntb-cntw,cntw-cntb);
    cnto+=cur;

    cout<<res+cnto<<"\n";

    return 0;
}
더 읽어보기 »

작성일 | In |

BOJ 22306

위 링크에서 문제 지문을 확인할 수 있다.

트리의 색깔과 쿼리 문제완 달리, 온라인으로 쿼리들을 처리해야 하는게 핵심이다.

이 글은 다음 개념들에 대한 지식을 독자가 이미 가지고 있다고 가정하고 서술한다.

  • offline query
  • tree의 euler tour traversal
  • tree의 dfs ordering
  • segment tree(index-tree)
  • small to large

원본 문제에선 offline으로 해결이 가능해 small to large를 적당히 활용하면 쉽게 풀 수 있다. 하지만 온라인으로 어떻게 할 지가 어렵다.

여러 가지 방식이 있을 것이고, 실제로 검수진 및 출제자의 풀이도 다양하다.

여기에선 내가 사용한 $O(nlog^{2}n+q)$풀이를 소개한다.

1번 쿼리를 어떻게 해결할지 생각해보자.

우선 오프라인일 때는 small to large를 역순으로 합쳐가면서 진행했으니, 지금은 역으로 small to large를 정점 집합을 분리시키면서 할 수 있지 않을까?라는 생각에서 시작한다.

그런 다음과 같은 두 가지 어려운 점이 있다.

1) 두 개로 쪼개지는 집합 중, 어느 집합이 더 작은 쪽인가? 2) 두 개로 나눠진 집합에서, 서로 다른 색깔의 개수를 어떻게 관리할 것인가?

우선 1)을 해결한다. 현재 어떤 정점 $a$에 대해서 그 부모 정점에 대해 끊는 상황이라 가정하자.

현재 $a$가 속해 있는 집합에 대해서, 그 정점들의 집합을 tree의 root에서 dfs 했을 때 나타나는 순서대로 정렬한 것을 $\lbrace v_{0}, v_{1}, \dots, v_{k-1} \rbrace$라고 하자. 그렇다면, $a$의 subtree에서 $a$와 같은 집합에 속해 있는 정점들의 indices는 구간을 이룬다. 즉, 어떤 $0 \leq i \leq j \leq k-1$에 대해 $i \sim j$이 $a$의 subtree에 속한 정점들의 indices가 된다. 이 사실에 착안하면, 풀이의 실마리를 찾을 수 있다.

이제 위의 $i,j$를 찾는 다면, $j-i+1$이 $a$의 subtree 중에서 현재 집합에 있는 정점들의 개수가 된다. 그러므로, $2(j-i+1) \geq k$라면, $a$의 subtree가 아니면서 현재 집합에 있는 정점들을 순회하면서 업데이트를 진행하고, $2(j-i+1) < k$이면 $a$의 subtree이면서 현재 집합에 속해 있는 정점들을 순회하면서 업데이트를 진행시키면 된다.

이를 효율적인 시간내에 구현할 수 있게 해주는 자료구조로는 set,map 등의 bbst 들과 segment tree가 있다.

2)의 경우, 이제 집합들을 분리할 수 있으므로, 각 집합에 대해 서로 다른 색깔이 얼마나 있는지 관리하고, 각각의 개수를 역시 배열이나 set등으로 관리하고, 업데이트의 경우 분리한 두 집합 중 작은 쪽의 정점을 돌며 업데이트 해주면 해결할 수 있다. 처음엔 서로 다른 색깔의 개수를 저장하고, 업데이트를 진행하며 어떤 색깔의 개수가 0이 되는 시점에 집합 내의 서로 다른 색깔의 개수를 하나 줄여주면 된다.

서로 다른 색깔의 개수는 정점의 개수를 넘을 수 없으므로, 정점, 색깔 모두 $O(nlogn)$에 비례하게 공간을 차지하게 만들 구현할 수 있다.

2번 쿼리는 이제 각 집합마다 색깔의 개수를 관리해주고 있으니, $O(1)$에 답변할 수 있다.

구현이 기므로, 주요 함수들과 배열에 대한 설명한다.

함수:

  • dfs() : 최초에 한번 호출되는 dfs 함수. tree를 순회하면서 dfs ordering 상으로 몇 번째인지 등을 정한다.
  • init() : 필요한 초기화 작업을 한다. 최초에 모든 정점들이 포함되어 있는 집합에 대한 업데이트 진행.
  • getsum() : 위에서 언급한 $j-i+1$값을 구해주는 역할
  • getid() : 주어진 범위에서 현재 집합에 남아 있는 정점이 있다면, 그것의 id, 즉 집합이 처음 생성 됐을 때, 그 집합 내에서 dfs ordering 순서가 몇 번째였는지 반환한다. 그렇지 않다면 INF를 return.
  • update_er() : segment tree에서 현재 지우고자 하는 정점에 관련된 정보를 업데이트.
  • update_add() : 집합을 두 개로 쪼갰을 때, 작은 쪽 집합의 정점에 대한 정보를 업데이트
  • update_set() : 1번 쿼리가 들어왔을 때, 새로운 집합을 만들고, 기존 집합에 대한 업데이트와 새로운 집합에 대한 초기화 작업을 진행한다.

배열:

  • id : 각 집합 내 정점의 dfs ordering에서의 순서를 순서대로 저장한다.
  • col: 각 집합이 최초로 생성됐을 때, 그 때의 서로 다른 색깔을 색깔 번호의 순서대로 저장한다.
  • cal: 각 집합의 색깔에 대해, 그 색깔이 현재 집합 내에 얼마나 있는지 그 개수를 저장한다.

자세한 구현은 다음 코드를 참고하면 된다. 시간 복잡도는 상기한 대로 $O(nlog^{2}n+q)$이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 1e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int par[MAXN];
int A[MAXN];

int in[MAXN];
int out[MAXN];
int ver[MAXN];

int bb[MAXN];

vector<int> id[MAXN];
vector<int> col[MAXN];

int cid[MAXN];

vector<int> cal[MAXN];
vector<int> tree[MAXN];
vector<int> caltree[MAXN];

int ccal[MAXN];

int seq = 0;

int snum = 0;

void dfs(int here){

    int there;

    in[here] = seq;
    seq++;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        dfs(there);
    }

    out[here] = seq-1;
    return;
}

void init(int n){

    graph = vector<vector<int> > (n+1);

    for(int i=2;i<=n;i++){
        graph[par[i]].push_back(i);
    }

    dfs(1);

    for(int i=1;i<=n;i++){
        ver[in[i]] = i;
    }

    for(int i=1;i<=n;i++){
        col[0].push_back(A[i]);
    }

    sort(col[0].begin(),col[0].end());
    col[0].erase(unique(col[0].begin(),col[0].end()),col[0].end());

    int csz = (int)col[0].size();

    ccal[0] = csz;

    cal[0] = vector<int> (csz);

    int cidx = -1;

    for(int i=1;i<=n;i++){
        cidx = lower_bound(col[0].begin(),col[0].end(),A[i])-col[0].begin();
        cal[0][cidx]++;
    }

    int base = 1;

    for(;base<n;base<<=1);

    bb[0] = base;

    tree[0] = vector<int> (base<<1,INF);
    caltree[0] = vector<int> (base<<1);

    for(int i=0;i<n;i++){
        tree[0][base+i] = i;
        caltree[0][base+i] = 1;
    }

    for(int i=base-1;i>=1;i--){
        tree[0][i] = tree[0][(i<<1)];
        caltree[0][i] = caltree[0][(i<<1)]+caltree[0][(i<<1)|1];
    }

    id[0] = vector<int> (n);

    for(int i=0;i<n;i++){
        id[0][i] = i;
    }

    return;
}

inline int getsum(int curid,int L,int R){

    int res = 0;

    while(L<=R){

        if(L&1){
            res += caltree[curid][L];
            L++;
        }
        if(!(R&1)){
            res += caltree[curid][R];
            R--;
        }
        L>>=1; R>>=1;
    }

    return res;
}

inline int getid(int curid,int L,int R){

    int res = INF;
    int rres = INF;

    while(L<=R){

        if(L&1){
            if(!(res^INF))res = tree[curid][L];
            L++;
        }
        if(!(R&1)){
            if(tree[curid][R]^INF)rres = tree[curid][R];
            R--;
        }
        L>>=1; R>>=1;
    }

    if(res^INF)return res;
    else return rres;
}

inline void update_er(int curid,int tmp){

    tree[curid][tmp] = INF;
    caltree[curid][tmp] = 0;
    tmp>>=1;

    while(tmp){

        tree[curid][tmp] = min(tree[curid][(tmp<<1)],tree[curid][(tmp<<1)|1]);
        caltree[curid][tmp] = caltree[curid][(tmp<<1)]+caltree[curid][(tmp<<1)|1];
        tmp>>=1;

    }

    return;
}

inline void update_add(int curid,int nxtid,int base,int idx){

    int curin = id[curid][idx];

    int curver = ver[curin];
    int curcol = A[curver];

    update_er(curid,base+idx);

    id[nxtid].push_back(curin);
    col[nxtid].push_back(curcol);

    return;
}

void update_set(int a){

    int curid = cid[a];

    int Lid = lower_bound(id[curid].begin(),id[curid].end(),in[a])-id[curid].begin();
    int Rid = upper_bound(id[curid].begin(),id[curid].end(),out[a])-id[curid].begin();

    Rid--;

    int base = bb[curid];

    int curtot = caltree[curid][1];

    int cursub = getsum(curid,base+Lid,base+Rid);

    snum++;
    int nxtid = snum;

    int idx = -1;

    if((cursub<<1)>=curtot){

        while(true){
            idx = getid(curid,base,base+Lid-1);

            if(idx^INF){
                update_add(curid,nxtid,base,idx);
            }
            else {
                break;
            }
        }

        while(true){
            idx = getid(curid,base+Rid+1,(base<<1)-1);

            if(idx^INF){
                update_add(curid,nxtid,base,idx);
            }
            else {
                break;
            }
        }
    }
    else {

        while(true){
            idx = getid(curid,base+Lid,base+Rid);

            if(idx^INF){
                update_add(curid,nxtid,base,idx);
            }
            else {
                break;
            }
        }

    }

    sort(col[nxtid].begin(),col[nxtid].end());
    col[nxtid].erase(unique(col[nxtid].begin(),col[nxtid].end()),col[nxtid].end());

    int nxtsz = (int)id[nxtid].size();
    int ncsz = (int)col[nxtid].size();

    int nxt_base = 1;

    for(;nxt_base<nxtsz;nxt_base<<=1);

    tree[nxtid] = vector<int> ((nxt_base<<1),INF);
    caltree[nxtid] = vector<int> ((nxt_base<<1));

    cal[nxtid] = vector<int> (ncsz);

    for(int i=0;i<nxtsz;i++){
        tree[nxtid][nxt_base+i] = i;
        caltree[nxtid][nxt_base+i] = 1;
    }

    for(int i=nxt_base-1;i>=1;i--){
        tree[nxtid][i] = tree[nxtid][(i<<1)];
        caltree[nxtid][i] = caltree[nxtid][(i<<1)]+caltree[nxtid][(i<<1)|1];
    }

    bb[nxtid] = nxt_base;

    int ncidx = -1;
    int nxtcol = 0;
    int nxtver = 0;

    for(int i=0;i<nxtsz;i++){
        nxtver = ver[id[nxtid][i]];
        nxtcol = A[nxtver];
        ncidx = lower_bound(col[nxtid].begin(),col[nxtid].end(),nxtcol)-col[nxtid].begin();

        cid[nxtver] = nxtid;

        cal[nxtid][ncidx]++;
    }

    ccal[nxtid] = ncsz;

    int ccidx = -1;

    for(int i=0;i<ncsz;i++){
        ccidx = lower_bound(col[curid].begin(),col[curid].end(),col[nxtid][i])-col[curid].begin();

        cal[curid][ccidx]-=cal[nxtid][i];
        if(!cal[curid][ccidx]){
            ccal[curid]--;
        }
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    int ty;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n>>q;

    for(int i=2;i<=n;i++){
        cin>>par[i];
    }

    for(int i=1;i<=n;i++){
        cin>>A[i];
    }

    init(n);

    int res = 0;

    for(int i=1;i<n+q;i++){
        cin>>ty>>k;

        a = k^res;

        if(ty&1){
            update_set(a);
        }
        else {
            res = ccal[cid[a]];
            cout<<res<<"\n";
        }
    }

    return 0;
}
더 읽어보기 »

작성일 | In |

결과 및 총평

내 제출현황과 순위는 위와 같다.

썩 만족스럽지 않은 결과였다. A에서 착각을 해서 시작부터 WA를 쌓아서 시작부터 느낌이 별로 좋지는 않았다…..

순위 역시 270위로, 아주 좋지 않은 성적이다. 실제로 지난 ARC 대회와 등수만으로 비교했을 때 퍼포먼스가 현재 내 레이팅과 비슷할 것이라 여겼고, 떨어질 것이라 예상했다. 하지만 어떻게 또 올라서(….) 또 max rating을 경신했다. 다음 주에 있는 ARC는 좀 더 잘쳐서, 2200을 넘길 수 있으면 좋겠다.

대회 문제들에 대한 얘기를 하자면 A,B는 ARC치고 좀 쉬운 난이도 였고, C,D는 살짝 어려웠다고 생각한다. C를 난 접근 조차 잘 못했고, D도 그렇게 까지 쉬운 문제는 아닌 듯. D 점수가 C 점수보다 높았고, 다행히 D를 그렇게 까지 많이 풀지 않아서 그나마 3이라도 오른 것 같다. E는 D와 점수가 같지만 어려운 문제인 듯.

아래는 A~D의 간단한 풀이와 코드이다. 이 중 C만 대회 풀이를 참고한 것이다. 문제들은 링크에서 확인 가능하다.

A. Arithmetic Sequence

세 수 $A_{0}, A_{1}, A{2}$가 주어지고, 원하는 만큼 세 수에 1씩을 더하는 연산을 시행할 수 있다. 이때, 세 수가 등차수열이 되려면 최소 몇 번을 시행해야 하는지 묻는 문제이다.

우선 편의상 $X_{0} = A_{1}-A_{0}, \ X_{1} = A_{2}-A_{1}$라고 두자. 그리고 각 $A_{i}$에 1을 더했을 때 어떤 일이 일어나는지 관찰한다.

  • $A_{0}$에 1을 더하는 경우: $X_{0}$이 1 감소한다.
  • $A_{1}$에 1을 더하는 경우: $X_{0}$이 1 증가하고, $X_{1}$이 1 감소한다.
  • $A_{2}$에 1을 더하는 경우: $X_{1}$이 1 증가한다.

위의 관찰을 응용하면, 다음과 같이 답이 나옴을 알 수 있다.

  • $X_{0} = X_{1}$인 경우, 이미 등차수열이므로 답은 $0$
  • $X_{0} > X_{1}$인 경우, $A_{0}$또는 $A_{2}$에 1을 더하면 $X_{0} - X_{1}$이 1씩 줄어들고, $A_{1}$에 1을 더하면 $X_{0} - X_{1}$이 2씩 증가한다. 그러므로, $A_{0}$또는 $A_{2}$에 1을 등차수열이 될 때까지 더하면 된다. 답은 $X_{0} - X_{1}$
  • $X_{0} < X_{1}$인 경우, $A_{0}$또는 $A_{2}$에 1을 더하면 $X_{1} - X_{0}$이 1씩 늘어나고, $A_{1}$에 1을 더하면 $X_{1} - X_{0}$이 2씩 감소한다. 그러므로 $X_{1} - X_{0}$이 짝수이면, $(X_{1} - X_{0})/2$가 답이 된다. 홀수이면, $X_{1} - X_{0}$이 1이 될 때까지 $A_{1}$에 1을 더하고, 그 후 $A_{0}, A_{1}$에 각각 1을 더하면 된다. $X_{1} - X_{0} = 2k+1$이면 답은 $k+2$이다.

이렇게 케이스를 나눠서 구현하면 끝. 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

int main()
{
    ll n,m,k,a,b,c,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
    ll res = 0;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>a>>b>>c;

    x = b-a;
    y = c-b;

    if(x==y){
        cout<<0<<"\n";
    }
    else if(x>y){
        cout<<x-y<<"\n";
    }
    else {
        k = y-x;
        if(k&1)cout<<((k>>1)+2)<<"\n";
        else cout<<(k>>1)<<"\n";
    }

    return 0;
}

B. Increasing Triples

어떤 의미에선 A보다도 쉬웠던 것 같다… 단순한 그리디가 성립한다. A를 작은 순서대로 보면서, 현재보고 있는 것보다 크면서 제일 작은 원소를 B에서 고르고, 그 고른 원소보다 크면서 제일 작은 원소를 C에서 고른 후, 이 과정을 반복한다. 더이상 그런 원소를 B또는 C에서 뽑을 수가 없으면 종료한다.

코드는 다음과 같다. 정렬 후 투 포인터처럼 순회하는 것도 가능하지만, 난 그냥 우선순위 큐를 써서 구현했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;
 
typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;
 
priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;
 
priority_queue<int> pqA;
priority_queue<int> pqB;
priority_queue<int> pqC;
 
 
int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;
 
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    cin>>n;
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqA.push(-x);
    }
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqB.push(-x);
    }
 
    for(int i=0;i<n;i++)
    {
        cin>>x;
        pqC.push(-x);
    }
 
    int idy = -1;
 
    for(int i=0;i<n;i++){
 
        cur = -pqA.top();pqA.pop();
 
        idx = -1;
 
        while(!pqB.empty()){
            idx = -pqB.top(); pqB.pop();
            if(idx>cur)break;
        }
 
        if(idx<=cur)break;
 
        idy = -1;
 
        while(!pqC.empty()){
            idy = -pqC.top(); pqC.pop();
            if(idy>idx)break;
        }
 
        if(idy<=idx)break;
 
        cnt++;
    }
 
    cout<<cnt<<"\n";
 
    return 0;
}

C. 1, 2, 3 - Decomposition

10진법으로 나타냈을 때 $1,2,3$ 밖에 나타나지 않는 수들의 합으로 주어진 수 $N$을 나타내려면 최소 몇 개가 필요한지 묻는 문제이다.

처음 봤을 때 어떻게 접근해야 하는지 몰랐었고, 끝날 때 까지 몰랐다..

official 풀이는 다음과 같다.

$f(N)$를 원하는 값을 도출하는 함수라고 하면, $f(N) \leq K$일 조건을 생각한다. 이때, $N = 10n+r$일 때, $K \leq r \leq 3K$이고, $f(n) \leq K$ 이면 된다. 증명은 생략한다.

어쨌든 위의 사실이 성립하므로, $f(N) \leq 5$가 성립함을 알 수 있다. $K = 5$ 면 $N = 10n+r$이고, $K \leq r \leq 3K$인 $n, r$이 존재할 수 밖에 없기 때문이다.

이제 이 사실을 이용하면 메모리제이션을 이용해 문제를 풀 수 있다.

좀 더 자세한 풀이를 원한다면 editorial을 참고.

코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

map<ll,int> mp;

int solve(ll x){
    if(mp.find(x)!=mp.end())return mp[x];
    if(x<0){
        return mp[x] = INF;
    }

    int cur = (x%10);

    int res = 5;
    int curv;

    if(!cur){
        if(solve((x-10)/10)<=4)res = 4;
    }
    else if(cur==1){
        if(solve((x-10)/10)<=4)res = 4;
        curv = solve(x/10);
        if(curv<=1)res = 1;
    }
    else if(cur==2){
        if(solve((x-10)/10)<=4)res = 4;
        curv = solve(x/10);
        if(curv<=2)res = curv;
    }
    else if(cur==3){
        curv = solve(x/10);
        if(curv<=3)res = curv;
    }
    else if(cur<=6){
        curv = solve(x/10);
        if(curv<=4)res = max(curv,2);
    }
    else {
        curv = solve(x/10);
        if(curv<=4)res = max(curv,3);
    }

    return mp[x] = res;
}

int main()
{
    ll n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    mp[0] = 0;

    for(int i=1;i<=3;i++)mp[i] = 1;
    for(int i=4;i<=6;i++)mp[i] = 2;
    for(int i=7;i<=9;i++)mp[i] = 3;

    while(tc--){

        cin>>n;

        int res = solve(n);

        cout<<res<<"\n";
    }

    return 0;
}

D. Inc, Dec - Decomposition

지문이 기므로, 자세한 내용은 문제 지문을 참고.

우선, $B_{i-1} \leq B_{i}$, $C_{i-1} \geq C_{i}$라는 성질 조건 때문에, $A_{i}-A_{i-1}$ 값이 양수면 $B_{i} - B_{i-1} \geq A_{i}-A_{i-1}$이고, 음수면 $C_{i}-C_{i-1} \leq A_{i}-A_{i-1}$임이 성립함을 알 수 있다. 그리고 $B_{i}$, $C_{i}$에 대해 $(i,B_{i})$와 $(i,C_{i})$를 도시한 그래프를 생각했을 때, 구하는 값과 그래프의 개형을 생각하면 다음 성질이 성립할 때 최소가 됨을 알 수 있다.

  • $A_{i}-A{i-1} \geq 0$이면 $B_{i} - B_{i-1} = A_{i}-A_{i-1}$이 성립하고, $A_{i}-A{i-1} < 0$이면 $C_{i}-C_{i-1} = A_{i}-A_{i-1}$이다.

그리고, 이제 위의 성질이 성립한다고 생각하고, 원하는 값인 $\sum_{i=1}^{N}(\left\lvert B_{i} \right\rvert + \left\lvert C_{i} \right\rvert)를 $B_{0}$에 대한 함수로 나타내면, 직선 여러개가 붙어 있는 모양의 함수가 됨을 쉽게 알 수 있다. 따라서 변곡점에 대해서 함수 값을 모두 구한 후, 그 최솟값을 구하면 된다.

여담으로, 난 상수 최댓값 등의 범위를 잘못 정해서 세 번이나 틀렸다…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e8+10;
const int MAXN = 2e5+10;
const ll LINF = 1LL*INF*MAXN;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

ll A[MAXN];
ll B[MAXN];
ll C[MAXN];
int cal[MAXN*3];
ll vv[MAXN*3];
char S[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>n;

    for(int i=0;i<n;i++){
        cin>>A[i];
    }

    for(int i=1;i<n;i++){
        if(A[i]>A[i-1]){
            B[i] = A[i]-A[i-1];
        }
        else {
            C[i] = A[i]-A[i-1];
        }
    }

    for(int i=1;i<n;i++){
        B[i]+=B[i-1];
        C[i]+=C[i-1];
    }

    vector<ll> pos;

    pos.push_back(-LINF);
    pos.push_back(LINF);

    for(int i=0;i<n;i++){
        pos.push_back(-B[i]);
        pos.push_back(-B[i]-1);
        pos.push_back(-B[i]+1);
        pos.push_back(A[0]+C[i]);
        pos.push_back(A[0]+C[i]-1);
        pos.push_back(A[0]+C[i]+1);
    }

    sort(pos.begin(),pos.end());
    pos.erase(unique(pos.begin(),pos.end()),pos.end());

    ll totv = 0;

    for(int i=0;i<n;i++){
        idx = lower_bound(pos.begin(),pos.end(),-B[i])-pos.begin();
        cal[idx]++;
        vv[idx]+=B[i];
        idx = lower_bound(pos.begin(),pos.end(),A[0]+C[i])-pos.begin();
        cal[idx]++;
        vv[idx]-=(A[0]+C[i]);

        totv -= B[i];
        totv += (A[0]+C[i]);
    }

    int psz = (int)pos.size();

    ll va = -(n<<1);

    ll res = 300LL*INF*INF;
    ll curv = 0;

    for(int i=0;i<psz-1;i++){

        va += (cal[i]<<1);
        totv += (vv[i]<<1);

        curv = va*pos[i]+totv;

        res = min(res,curv);
    }

    cout<<res<<"\n";

    return 0;
}
더 읽어보기 »

작성일 | In |

결과 및 총평


어제 오후 3시에 거의 바로 시작했고, 저녁 먹기 전에 끝내려고 했다. 약간 설렁설렁했는데, 어쨌든 6시 전에 올솔브에, 전부 한번에 맞았다. 그래서 기분 좋게 저녁 먹으러 갔었다.

종료 후 전체 솔브 수는 차레로 1305/661/315/232/147였다.

솔브 수에서 보이듯 예년 보다 전체적으로 난이도가 쉬웠다. 작년 Round2 제출자가 500명을 살짝 넘은 것으로 보이는데, 올해는 1,2번 모두 만점 받은 사람이 500을 훨씬 넘긴 것을 보면, 어떻게 될진 모르겠지만 3번까지 긁기는 해야 안심할 수 있지 않을까 싶다.

아래는 각 문제의 간단한 풀이와 코드이다. 문제 지문은 나중에 codeground의 practice에 올라올 테니, 여기선 독자가 문제를 읽었다고 가정한다.

1. 친구들

각 사람을 정점으로 생각하고, 친구 관계를 간선으로 이어진 것이라 생각하면 결국 이 graph에서, connected component는 완전 그래프(perfect graph)가 된다. 따라서 연결 컴포넌트 개수가 곧 정답이 된다. 이는 union-find나 dfs로 쉽게 구현 가능하다. 나의 경우 dfs를 사용해 컴포넌트 수를 세었다. connected component만 판단하면 되니, 봐야 하는 간선은 각 $i$에 대해 $i$와 $i+D_{i}$를 있는 간선 밖에 없다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
bool vis[MAXN];
char S[MAXN];

void dfs(int here)
{
    vis[here] = true;

    int there;

    for(int i=0;i<(int)graph[here].size();i++){
        there = graph[here][i];
        if(vis[there])continue;
        dfs(there);
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    for(int runs=1;runs<=tc;runs++){

        cin>>n;

        for(int i=1;i<=n;i++){
            cin>>A[i];
        }

        graph = vector<vector<int> > (n+1);

        for(int i=1;i<=n;i++){
            cur = i+A[i];
            if(cur>n)continue;
            graph[i].push_back(cur);
            graph[cur].push_back(i);
        }

        fill(vis,vis+n+1,false);

        cnt = 0;

        for(int i=1;i<=n;i++){
            if(vis[i])continue;
            cnt++;
            dfs(i);
        }

        cout<<"Case #"<<runs<<"\n";
        cout<<cnt<<"\n";
    }


    return 0;
}

2. 이진수

살짝 귀찮았던 문제, 결국 각 $b_{i}$는 $a_{i-t} or a_{i+t}$로 정해진다는 것을 알 수 있다. 그러므로 역추적을 위해서 다음과 같이 하면 된다.

  • $b_{i} = 0$인 경우, $a_{i-t},a_{i+t}$ 모두 (존재한다면) 0으로 정한다.
  • $b_{i} = 1$이고, $a_{i-t},a_{i+t}$ 중 한 쪽이 없거나, 한 쪽이 0으로 정해진 경우, 다른쪽엔 1로 값을 정한다.
  • $a_{i}$ 중 아직 정해지지 않은 값들에 대해서, greedy하게 앞에서 부터 순서대로 보면서, 아무렇게 해도 상관없다면 (그런 문자열이 존재한다면) 0으로, 반드시 1로 해야 한다면 1로 정해준다.

자세한 부분은 구현을 참고.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];
char T[MAXN];

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    for(int runs=1;runs<=tc;runs++){

        cin>>n>>k;
        cin>>S+1;

        fill(A,A+n+1,-1);

        for(int i=1;i<=n;i++){
            if(S[i]=='0'){
                if(i>k)A[i-k] = 0;
                if(i+k<=n)A[i+k] = 0;
            }
        }

        bool judge = true;

        for(int i=1;i<=n;i++){
            if(S[i]=='1'){
                if(i>k&&i+k<=n){
                    if(A[i-k]==0)A[i+k] = 1;
                    else if(A[i+k]==0)A[i-k] = 1;
                }
                else if(i>k){
                    A[i-k] = 1;
                }
                else if(i+k<=n){
                    A[i+k] = 1;
                }
            }
        }

        for(int i=1;i<=min((k<<1),n);i++){
            if(A[i]==-1)A[i] = 0;
        }

        for(int i=k+1;i<=n;i++){
            if(S[i]=='1'){
                if(i+k<=n&&A[i+k]==-1){
                    A[i+k] = 1^A[i-k];
                }
            }
        }

        for(int i=1;i<=n;i++){
            if(A[i]==-1)T[i] = '0';
            else T[i] = A[i]+'0';
        }
        T[n+1] = 0;

        cout<<"Case #"<<runs<<"\n";
        cout<<T+1<<"\n";
    }

    return 0;
}

3. No Cycle

그냥 가능한 정답을 묻는다면, 전체를 위상 정렬 시킨 후, 각 정점의 위상정렬상에서의 순서만 따져서 정답을 작성해도 된다. 하지만 이 문제에선 사전순으로 최소라는 조건이 붙으므로, 위와 같은 방식은 WA를 낸다. 다시 제한을 보면 $N \leq 500$, $M, K \leq 2000$으로 그렇게 크지 않다는 것을 알 수 있다. 그러니 각 간선의 방향을 결정할 때 마다 간선을 추가시켜 주면서, 지금 현재 정방향(결과에서 0으로 나타나는 방향)으로 추가가 가능한지 보고, 가능하면 정방향으로, 그렇지 않다면 역방향으로 간선 방향을 정해주면 된다. 이때 가능한지 판단은 dfs를 통해 했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];

bool vis[MAXN];
pii edge[MAXN];
char S[MAXN];

void dfs(int here){

    int there;

    vis[here] = true;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(!vis[there])dfs(there);
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    for(int runs=1;runs<=tc;runs++){

        cin>>n>>m>>k;

        graph = vector<vector<int> > (n+1);

        for(int i=0;i<m;i++){
            cin>>x>>y;
            graph[x].push_back(y);
        }

        for(int i=0;i<k;i++){
            cin>>edge[i].f>>edge[i].s;
        }

        for(int i=0;i<k;i++){

            fill(vis,vis+n+1,false);

            a = edge[i].f;
            b = edge[i].s;

            dfs(b);

            if(vis[a]){
                S[i] = '1';
            }
            else {
                S[i] = '0';
                graph[a].push_back(b);
            }
        }
        S[k] = 0;

        cout<<"Case #"<<runs<<"\n";
        cout<<S<<"\n";
    }


    return 0;
}

4. 예약 시스템

이 문제의 핵심은 $p(c) = w_{a}+w_{b}$이므로, 그룹 마다 스트레스를 따로 따로 생각할 수 있단 점이다. 결국 총 페널티는 각 그룹에 대해, 그룹에서 다른 그룹과 이웃한 개수가 몇 개인지에 따라 달려 있다. 간단히 생각해 보면 같은 그룹 끼리 뭉쳐 있을 수록 페널티가 작아질 것이라 생각할 수 있다. (문제를 풀 당시엔 이렇게 생각했는데, 반례가 존재한다고 한다. 그리고 문제도 수정됐다…) 짝수개일 때는 직사각형 모양, 홀수일 경우 직사각형에서 정사각형 하나가 붙어 있는 모양이다. 이때 그룹의 인원 수가 작으면 계산이 달라질 수 있지만, 다행히 각 그룹 인원 수가 5이상이기 때문에, 달라지지 않는다.

이제 남은 것은 적절한 case-work이다. 양 끝에 있는 그룹의 인원수가 홀수/홀수 인 경우, 짝수/짝수 인 경우, 홀수/짝수 인 경우로, 나누어, 각각의 최솟값을 구해서 전체 최솟값을 구하면 된다. 제한에서 홀수인 그룹의 개수는 짝수가 될수 밖에 없음에 유의하라.

자세한 부분은 역시 코드를 참고.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

int A[MAXN];
char S[MAXN];

vector<int> val[MAXN];

ll getbotheven(int n){

    int evencnt = 0;

    for(int i=1;i<=n;i++){

        if(!(A[i]&1))evencnt++;

    }

    if(evencnt<2)return LINF;

    ll mx = 0;
    ll mx2 = 0;
    ll curmx = 0;
    ll curv = 0;
    ll tot = 0;

    for(int i=1;i<=n;i++){

        if(A[i]&1){
            curv = (val[i][0]<<1)+val[i][1]+val[i][2]+val[i][3];
            curmx = 0;
        }
        else {
            curv = val[i][0]+val[i][1]+val[i][2]+val[i][3];
            curmx = val[i][2]+val[i][3];
        }
        tot += curv;
        if(mx<curmx){
            mx2 = mx;
            mx = curmx;
        }
        else {
            mx2 = max(mx2,curmx);
        }
    }

    tot-=(mx+mx2);

    return tot;
}

ll getbothodd(int n){

    int oddcnt = 0;

    for(int i=1;i<=n;i++){
        if(A[i]&1)oddcnt++;
    }

    if(!oddcnt)return LINF;

    ll curv = 0;
    ll tot = 0;
    ll mx = 0;
    ll mx2 = 0;
    ll curmx = 0;

    if(oddcnt==2){

        for(int i=1;i<=n;i++){

            if(A[i]&1){
                curv = (val[i][0]<<1)+val[i][1];
            }
            else {
                curv = (val[i][0]<<1)+(val[i][1]<<1)+val[i][2]+val[i][3];
            }
            tot += curv;
        }
    }
    else {

        for(int i=1;i<=n;i++){

            if(A[i]&1){
                curv = (val[i][0]<<1)+val[i][1]+val[i][2]+val[i][3];
                curmx = val[i][2]+val[i][3];
            }
            else {
                curv = val[i][0]+val[i][1]+val[i][2]+val[i][3];
                curmx = 0;
            }

            tot += curv;
            if(mx<curmx){
                mx2 = mx;
                mx = curmx;
            }
            else {
                mx2 = max(mx2,curmx);
            }
        }

        tot-=(mx+mx2);
    }

    return tot;
}

ll getdiff(int n){

    int oddcnt = 0;

    for(int i=1;i<=n;i++){
        if(A[i]&1)oddcnt++;
    }

    if(!oddcnt)return LINF;
    if(oddcnt==n)return LINF;

    ll oddmx = 0;
    ll evenmx = 0;
    ll curmx = 0;
    ll curv = 0;
    ll tot = 0;

    for(int i=1;i<=n;i++){

        if(A[i]&1){
            curv = (val[i][0]<<1)+val[i][1]+val[i][2]+val[i][3];
            curmx = val[i][2]+val[i][3];
            oddmx = max(oddmx,curmx);
        }
        else {
            curv = val[i][0]+val[i][1]+val[i][2]+val[i][3];
            curmx = val[i][2]+val[i][3];
            evenmx = max(evenmx,curmx);
        }
        tot += curv;
    }

    tot-=(oddmx+evenmx);
    return tot;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    for(int runs=1;runs<=tc;runs++){

        cin>>n>>m;

        for(int i=1;i<=n;i++){

            cin>>k;

            val[i].clear();
            A[i] = k;

            for(int j=0;j<k;j++){
                cin>>x;
                val[i].push_back(x);
            }

            sort(val[i].begin(),val[i].end());
        }

        ll res = LINF;

        if(n==1){
            res = 0;
        }
        else {
            res = min(res,getbotheven(n));
            res = min(res,getbothodd(n));
            res = min(res,getdiff(n));
        }

        cout<<"Case #"<<runs<<"\n";

        cout<<res<<"\n";
    }

    return 0;
}

5. 차이

가장 어려운 문제이면서도, 가장 전형적인 문제 였다고 생각한다.

문제의 어투(?)에서 느낄 수 있듯이 1번 쿼리에서, 정점 $i$와 $j$를 간선으로 있는 것처럼 생각할 수 있다. 물론 방향에 따라 가중치의 부호는 달라진다.

이제 2번 쿼리에서, NC인지 아닌지 부터 판단해보자. 어떤 정점 $i$와 $j$가 하나의 connected component 안에 있다면, 문제에서 주어진 것처럼 경로를 구성할 수 있음을 알 수 있다. 따라서, 하나의 connected component안에 있다면, NC가 아니고, 그렇지 않다면 NC 이다.

다시 1번 쿼리로 돌아가서, $i$와 $j$를 이으려 하는 상황을 보자. $i$와 $j$가 다른 connected component 안에 있으면 그냥 이어주면 된다. 같은 connected component라면 이제, $X_{i}-X_{j}$를 알아낼 수 있으므로, 업데이트 하려는 정보와 구한 정보를 비교한다. 만약에 같다면, 앞으로도 유일하게 결정 가능하므로 넘어간다. 하지만 다르다면, 지금 component내의 임의의 정점 $a,b$에 대해 $X_{a}-X_{b}$가 유일하게 결정되지 않는다. 따라서, 이 component에서 유일하게 결정할 수 없다고 표시해주어야 한다. 이후 2번 쿼리가 들어왔을 때, 같은 component 안에 있기는 하나 그 component에 이 표시가 되어 있다면 CF를 출력하면 된다.

이제 NC,CF 도 아닌 경우에 어떻게 구하는지 본다. 먼저 1번 쿼리에서 $i$와 $j$를 이을 때, 같은 component라면 간선을 추가할 필요가 없다는 것을 쉽게 알 수 있다. 따라서, graph의 형태는 forest가 된다. 쿼리들을 online으로 처리하는 것이 강제된다면 link-cut tree 같은 어려운 자료구조를 써야하지만, 지금같이 모든 정보가 주어지는 경우에는 그럴 필요가 없다. 최종 forest의 형태가 주어져 있으므로, 그에 따라 구성하면 된다.

구현하는 방법에는 여러 가지가 있겠지만, 나의 경우 전체 forest를 0번 정점을 추가해서 하나의 tree로 만든 후, dfs ordering + indextree를 사용해서 구했다. 그 외에 NC, CF 등의 판단은 union-find를 사용했다. union-find에서 union을 할 때 conflict 정보를 넘겨주어야 함에 유의하라.

자세한 구현은 코드 참고.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
#include <bits/stdc++.h>
#define f first
#define s second
#define MOD 1000000007
#define PMOD 998244353
#define pb(x) push_back(x)
using namespace std;

typedef long long int ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> plii;
typedef pair<int, pii> piii;
const int INF = 1e9+10;
const ll LINF = 1LL*INF*INF;
const int MAXN = 2e5+10;
const int MAXM = 5e3+10;

priority_queue<int> pq;
vector<vector<int> > graph;
queue<int> que;

pii query[MAXN];
ll val[MAXN];
int ty[MAXN];

int par[MAXN];

int pp[MAXN];
int in[MAXN];
int out[MAXN];

bool iscon[MAXN];

ll tree[MAXN*4];

int root(int x){
    if(par[x]==x)return x;
    else return par[x] = root(par[x]);
}

int seq;

void dfs(int here,int p){

    int there;

    in[here] = seq;
    seq++;

    for(int i=0;i<graph[here].size();i++){
        there = graph[here][i];
        if(there==p)continue;
        pp[there] = here;
        dfs(there,here);
    }

    out[here] = seq-1;

    return;
}

inline void update(int L,int R,ll v){

    while(L<=R){

        if(L&1){
            tree[L]+=v;
            L++;
        }
        if(!(R&1)){
            tree[R]+=v;
            R--;
        }
        L>>=1; R>>=1;
    }

    return;
}

inline ll getans(int tmp){

    ll res = 0;

    while(tmp){
        res += tree[tmp];
        tmp>>=1;
    }

    return res;
}

inline ll getdis(int base,int a,int b){

    ll ansa = getans(base+in[a]);
    ll ansb = getans(base+in[b]);

    return ansa-ansb;
}

void solve(int n,int m){

    int a,b;
    int x,y;

    graph = vector<vector<int> > (n+1);

    for(int i=1;i<=n;i++){
        par[i] = i;
    }

    for(int i=0;i<m;i++){
        if(ty[i]==2)continue;

        x = query[i].f;
        y = query[i].s;

        a = root(x);
        b = root(y);

        if(a^b){
            par[b] = a;
            graph[x].push_back(y);
            graph[y].push_back(x);
        }

    }

    for(int i=1;i<=n;i++){
        if(par[i]==i){
            graph[0].push_back(i);
            graph[i].push_back(0);
        }
    }

    seq = 0;

    dfs(0,-1);
    pp[0] = -1;

    int base = 1;

    for(;base<=n;base<<=1);

    fill(tree,tree+(base<<1),0);

    fill(iscon,iscon+n+1,false);

    for(int i=1;i<=n;i++){
        par[i] = i;
    }

    ll curd = 0;

    for(int i=0;i<m;i++){

        x = query[i].f;
        y = query[i].s;

        a = root(x);
        b = root(y);

        if(ty[i]==1){

            if(a^b){
                par[b] = a;
                iscon[a] |= iscon[b];

                if(pp[x]==y)update(base+in[x],base+out[x],val[i]);
                else update(base+in[y],base+out[y],-val[i]);
            }
            else {

                curd = getdis(base,x,y);

                if(curd!=val[i])iscon[a] = true;
            }
        }
        else {

            if(a^b){
                cout<<"NC\n";
            }
            else {
                if(iscon[a])cout<<"CF\n";
                else {
                    curd = getdis(base,x,y);
                    cout<<curd<<"\n";
                }
            }
        }
    }

    return;
}

int main()
{
    int n,m,k,a,b,x,y,q;
    int sum = 0;
    int cnt = 0;
    int mx = 0;
    int mn = INF;
    int cur = 0, idx = -1;
    int tc;

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin>>tc;

    for(int runs=1;runs<=tc;runs++){

        cin>>n>>m;

        for(int i=0;i<m;i++){
            cin>>ty[i];
            if(ty[i]&1){
                cin>>query[i].f>>query[i].s>>val[i];
            }
            else {
                cin>>query[i].f>>query[i].s;
            }
        }

        cout<<"Case #"<<runs<<"\n";

        solve(n,m);
    }

    return 0;
}
더 읽어보기 »

작성일 | In |

개요

블로그가 너무 심각하게 비활성화 돼있는 것 같아서.. 근황이나마 간단하게 남기려고 한다.

학교 생활

3학년을 맞아 전공필수 2개를 포함한 전공과목 3개, 교양과목 3개를 듣고 있다. 서울대 컴공 내에선 악명 높은(?) 과목 두 개인 소프트웨어 개발의 원리와 실습(소개원실)과 시스템 프로그래밍(시프)를 동시에 수강하고 있는데, 왜 동시에 듣지 말라는지 알 것 같다… 다른 과목 하나도 점점 어려워져서 학기 초에 열심히 하지 않은 대가를 치를 예정. 나머지 교양들은 그럭저럭 듣고 있다. 점점 로드가 쌓이면서 학교생활이 빡빡해지고 있다.

PS

원래 올해의 목표 중 하나가 1일 1다이아 솔브 였는데, 연초~3월 중순까지는 열심히 해서 solved.ac 기준으로 다이아 300개를 돌파하는데 성공했다. atcoder에서도 연속으로 음이 아닌 레이팅 변화를 기록하며 max rating을 찍었다. 다만 중간 고사와 과제가 시작되면서 현재는 예전만큼 열심히 하지 못하고 있다. 그 여파로(?) gcj 1A에서 1300등대의 다소 아쉬운 성적을 기록했다. 2라운드에는 가겠지만, 이대로는 티셔츠 수령 가능성이 매우 낮아 보인다. 전체적으로 PS/CP 감이 떨어진 것 같은데, 틈을 내서라도 공부를 진행할 필요성을 느낀다. snups에서 스터디를 진행한다는데, 참가하면 억지로라도 공부하게 되지 않을까 싶다.

동아리(개발)

서울대의 학내 동아리 중 wafflestudio에서 프로젝트 하나에 참가하고 있는데, 학기가 진행되면서 기여를 거의 못하고 있다. 빨리 과제들 정리하고 참가해야지..

기타

요즘엔 잠도 많이 오고, 전체적으로 체력이 많이 떨어진 것 같다. 관리가 필요할 듯.

더 읽어보기 »

작성일 | In |

총평

문제들은 다음 링크에서 확인할 수 있다.

https://atcoder.jp/contests/abc191/tasks

평소보다 어려운 ABC 였다. 결국 올솔에 실패했다. 전체 순위 162위, 퍼포먼스 2357로 준수한 성적을 냈다.

A

계산 후 범위를 비교하면 되는 문제다.

B

입력 받은 순서대로 주어진 x 와 다르면 출력.

C

조건 때문에 쉬운 문제. 꼭짓점의 개수 = 변의 개수가 되므로, 꼭짓점의 개수를 세어주면 된다.

D

귀찮은 문제… 결국 많아봤자 소수점 넷째 자리까지 가므로, 10000 곱하면 된다. 대칭성이 성립하므로, X,Y 좌표 모두 절댓값으로 생각해도 무방하다. 그 뒤 가능한 x 범위에 대해 y 범위를 구할 수 있으므로, 잘 계산하면 된다.

E

많이 전형적인 문제. 그냥 N 번 다익스트라를 돌리면 해결된다.

더 읽어보기 »